ОСНОВНЫЕ РАСПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Говорят, что СВ x имеет биноминальное распределение, если
ее возможные значения 0,1,2,…,n , а соответствующие вероятности ![]()
Пример. Производится 4 выстрела по мишени. Вероятность попадания при одном выстреле 0,7. Найти закон распределения числа попаданий в мишень.
Случайная величина x - число попаданий в мишень. Ряд распределения имеет вид
|
x |
0 |
1 |
2 |
3 |
4 |
|
Р |
0,0081 |
0,0756 |
0,2646 |
0,4116 |
0,2401 |
р = 0,7, n = 4, q = 0,3
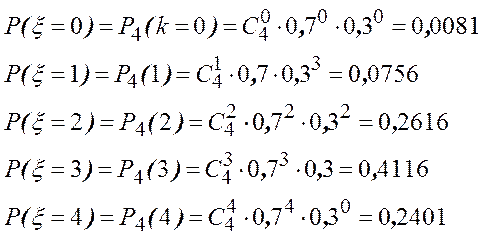
Найдем числовые характеристики.
Пусть ![]() – число наступлений события
– число наступлений события ![]() в
в ![]() -том
испытании.
-том
испытании.
|
Значения |
0 |
1 |
|
Вероятности |
q |
p |
![]() – независимые СВ, при этом
– независимые СВ, при этом ![]() .
.
Математическое ожидание
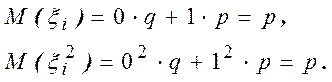
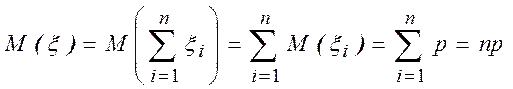 .
.
Дисперсия
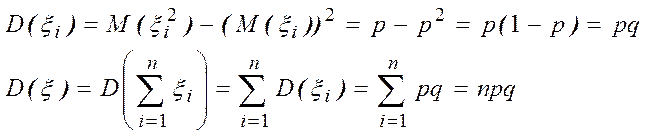
Говорят, что СВ x имеет
распределение Пуассона, если ее возможные значения 0,1,2,…,n , и
соответствующие вероятности 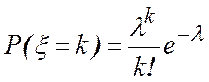 , где
, где ![]() - параметр распределения.
- параметр распределения.
Найдем 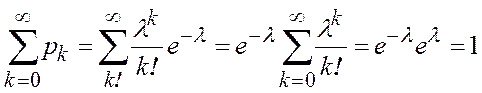
Распределение Пуассона широко используется в приложениях, особенно в теории массового обслуживания (число вызовов скорой помощи, число приходов посетителей в магазины).
Пример. Механизм включает в себя большое количество независимо работающих элементов с одинаковой вероятностью их отказа. Найти среднее число l отказов элементов, если вероятность того, что откажет хотя бы один элемент, равна 0,98.
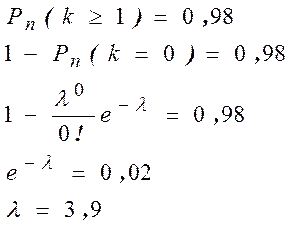
Значит, среднее число отказавших элементов примерно равно 4.
Математическое ожидание
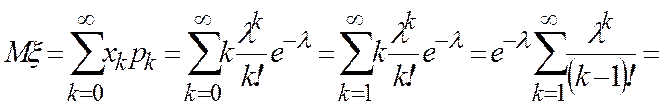
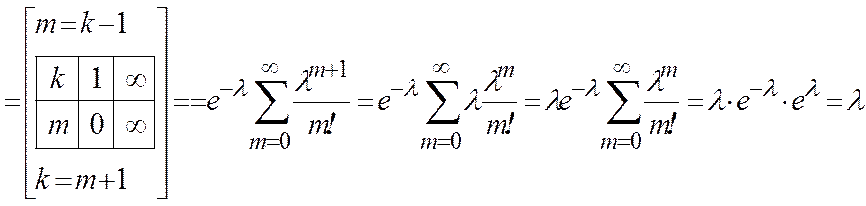 .
.
Дисперсия
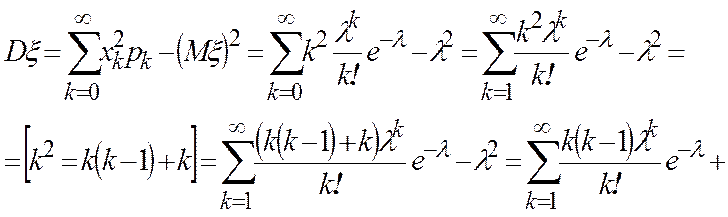
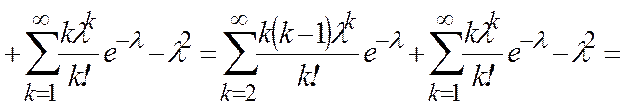
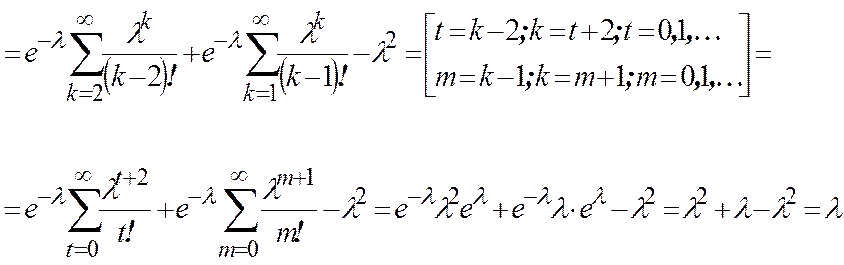
Говорят, что СВ x имеет геометрическое
распределение, если она принимает значения 0,1,2,…,n с вероятностями ![]()
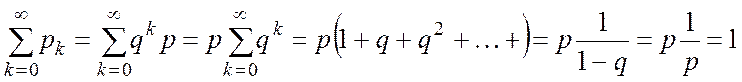
Пример. Производится стрельба по мишени до первого попадания. Построить ряд распределения числа промахов, если вероятность попадания в мишень при одном выстреле равна р.
Случайная величина x – число промахов до первого попадания.
|
x |
0 |
1 |
2 |
3 |
… |
|
р |
p |
pq |
q2p |
q3p |
… |
Математическое ожидание
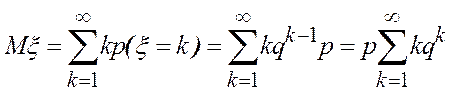
Поскольку члены ряда 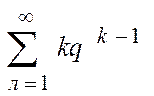 являются производными
соответствующих членов ряда
являются производными
соответствующих членов ряда 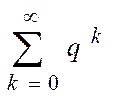 и
и 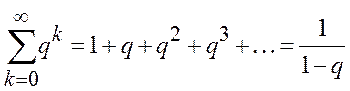 , то
, то
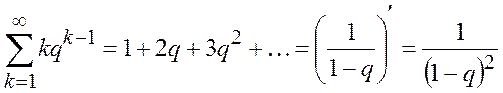
Следовательно,
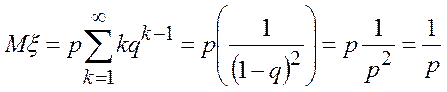
Дисперсия
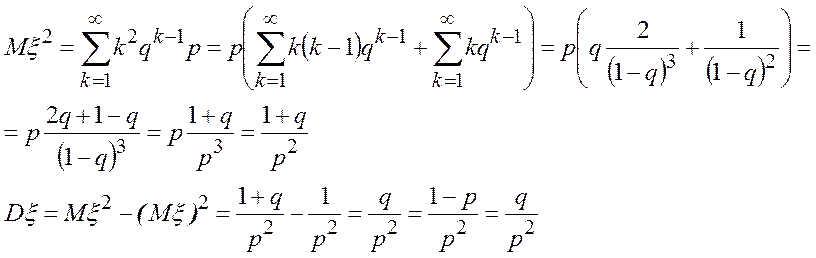
Геометрическое распределение +1 возникает при решении задач следующего типа.
Пример. Производится
стрельба по мишени до первого попадания. Случайная величина ![]() -
число израсходованных патронов до первого попадания. Найти закон распределения.
-
число израсходованных патронов до первого попадания. Найти закон распределения.
|
h |
1 |
2 |
3 |
… |
|
Р |
р |
qp |
q2p |
… |
Математическое ожидание
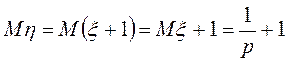
Дисперсия
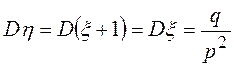
Говорят, что СВ x имеет равномерное распределение на отрезке [a; b] если ее плотность вероятности имеет вид:
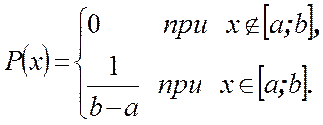 .
.
Найдем функцию распределения:
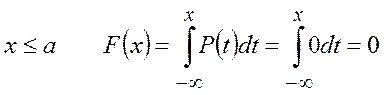 ,
,
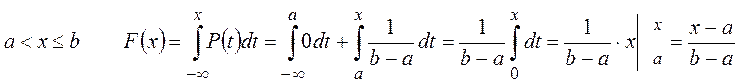 ,
,
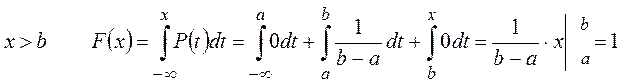 .
.
Тогда
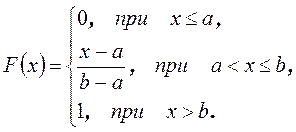
Равномерное распределение имеют СВ, которые характеризуют ошибки измерения с помощью инструментов с редкими делениями (когда значение округляется до ближайшего целого: при измерении расстояния между городами).
Математическое ожидание
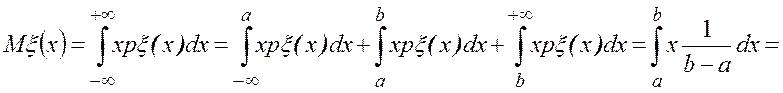
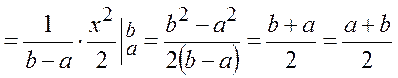
Дисперсия
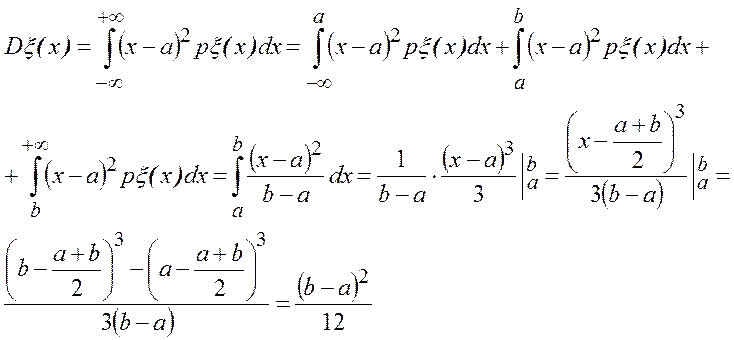
Говорят, что СВ x имеет показательное распределение с параметром l, если плотность вероятности имеет вид:
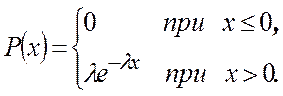
Найдем функцию распределения:
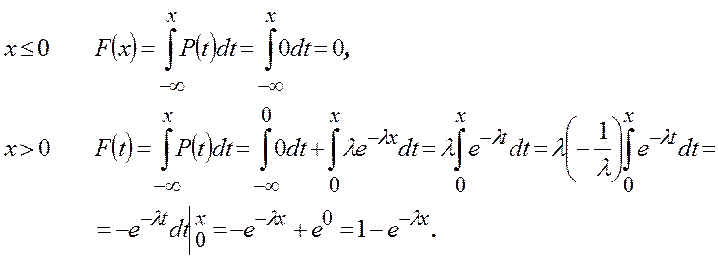
Тогда 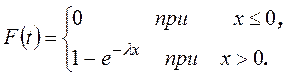
Показательное распределение имеют СВ, характеризующие время работы электрической лампочки или интенсивность обслуживания клиентов одним мастером.
Математическое ожидание
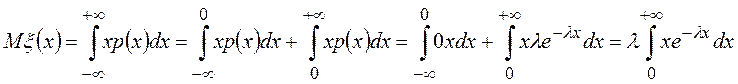 .
.
Применяем формулу интегрирования по частям:
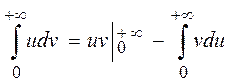 .
.
Полагаем ![]() .
.
Тогда
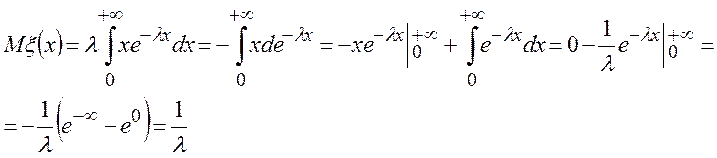
Дисперсия
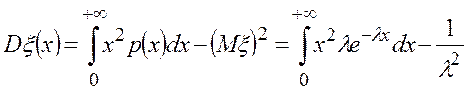
Дважды интегрируя по частям:
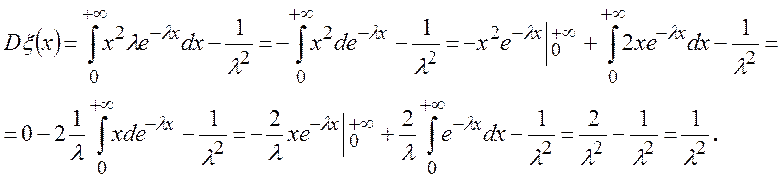
Говорят, что СВ x имеет нормальное
распределение с параметрами ![]() , если плотность
вероятности x имеет вид:
, если плотность
вероятности x имеет вид: 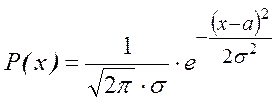 , хÎR. Если
, хÎR. Если ![]() ,
, ![]() , то
, то 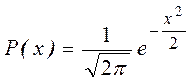 и СВ x
называется стандартной нормально распределенной.
и СВ x
называется стандартной нормально распределенной. ![]()
Функция распределения:
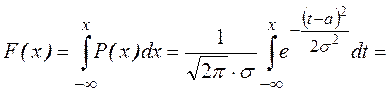
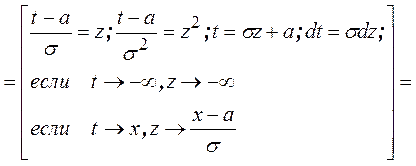
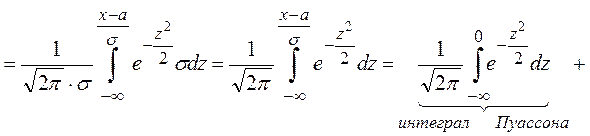
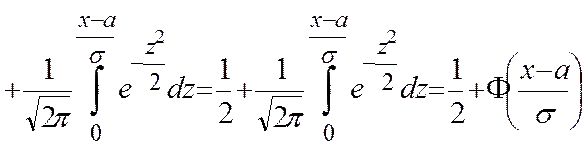
Получим 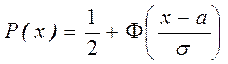 ,
где
,
где ![]() - интегральная функция Лапласа
- интегральная функция Лапласа
Значит, функцию распределения можно найти по
таблице значений ![]() .
.
Если ![]() и
и ![]() , то
, то 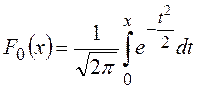 .
.
Математическое ожидание
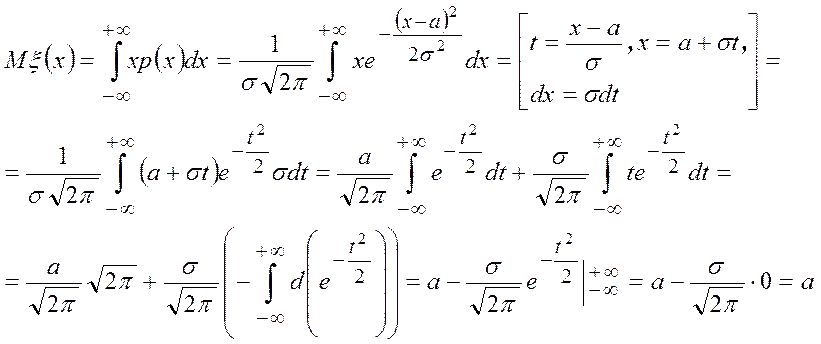
Дисперсия
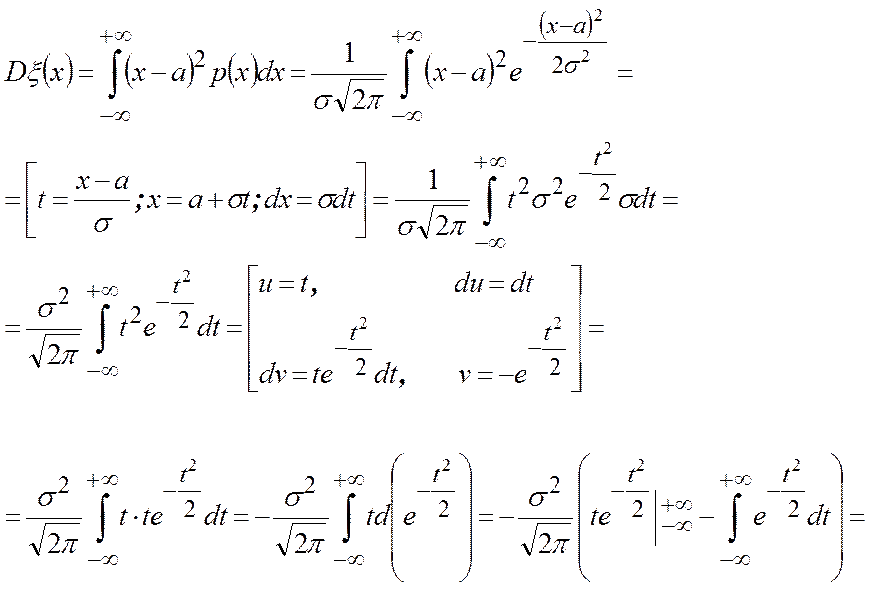
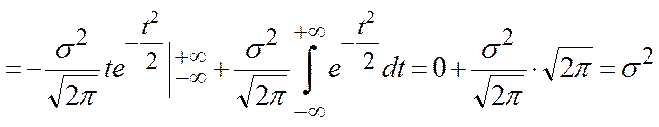
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.