Методические указания к лабораторному практикуму по курсу «Методика преподавания физики в школе», страница 4

Алгоритмы измерений и обработки полученных результатов. Прямые измерения. Метод среднего арифметического.

1. Проводят несколько измерений искомой величины x (при неизменных условиях опыта).

2. Определяют наиболее достоверное значение измеряемой величины:

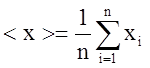
3.Вычисляют модули отклонения каждого результата от сред­него:

4. Определяют среднюю абсолютную погрешность:

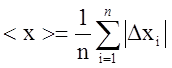
5. Оценивают случайную погрешность:

 при n ≥ 10

 при n = 5

 при n = 7;8.

6. Оценивают инструментальную погрешность:

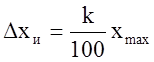 или  (или ).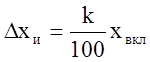

7. Оценивают погрешность отсчета:

8. Оценивают погрешность вычисления:

.

9. Оценивают полную погрешность:

10. Оценивают относительную погрешность:

%.

11. Учитывают поправку на систематическую погрешность:

.

12. Результат измерения записывают в интервальной форме:

.

Оценка погрешности косвенно измеряемой величины

(дифференциальный метод границ погрешностей)

Рассмотрим сначала простейший случай, когда функция у за­висит только от одного аргумента х, т.е.   

                                                         (1)

Величина х измеряется прямым методом, а у косвенным: вы­числяется по формуле (1). Если величина х измерена с абсолютной погрешностью , то величина у также будет определена с некото­рой погрешностью . При малых погрешностях = tgα·Δх, где  α – угол между касательной к кривой у = f(х) и осью абсцисс. Но тангенс угла наклона касательной к оси абсцисс равен производной от функции у в соответствующей точке, т.е. tgα = у'. Поэтому

                                         (2)

Поскольку значение у' может быть отрицательным, а абсо­лютная погрешность  всегда положительна, в соотношении (2) производную  нужно заменить ее модулем :

                                        (3)

Таким образом, чтобы вычислить абсолютную погрешность  косвенно измеряемой величины у, нужно абсолютную погрешность  величины, измеренной прямым методом, умножить на модуль производной

Значение производной у' должно вычисляться при истинном значении x, т.е. при x = х_ист. Но оно экспериментатору не известно. По этой причине на практике  приходится вычислять при х = x_изм. Такое приближение оправдано тем, что обычно погрешно­сти измерений не очень велики.

Теперь рассмотрим случай, когда у зависит от нескольких ар­гументов: у = f(x₁,x₂,…,x_N). Все величины х_i, (i == 1, 2,..., N) изме­ряются независимыми прямыми методами, а у – косвенным. Пусть абсолютные погрешности прямых измерений соответственно равны. Это приведет к погрешности . Если бы при пря­мых измерениях с некоторой погрешностью была определена толь­ко одна величина х₁, а остальные x₂,x₃,…,x_N были бы найдены точно, то в соответствии с формулой (3) абсолютная погрешность косвенно измеряемой величины была бы равна

                                     (4)

где  – частная производная от функции у по аргументу х₁ .т.е. производная от у по х₁ в предположении, что все остальные аргу­менты (х₂,х₃,...,x_N) постоянные,  – абсолютная погрешность из­мерения x₁.

Рассуждая аналогично относительно других величин х_i, (i = 2, 3,...,N), приходим к выводу, что каждая погрешность , вносит свой вклад в погрешность величины у, которую можно оценить по формуле

                                        (5)

Тогда общая погрешность , обусловленная неточным изме­рением всех аргументов х_i, будет равна сумме соответствующих ча­стных погрешностей (5):

                          (6)

В формуле (6) суммирование проводится потому, что под  понимается максимальная абсолютная погрешность, т.е. ее верхняя граница, что осуществляется тогда, когда все погрешности , вы­зывают отклонение величины у в одну сторону, например, в сторо­ну ее завышения.

Подставив в равенство (6) значение всех слагаемых, найден­ных в формуле (5), получим

.                (7)

Эта формула является основной для определения абсолютной погрешности косвенно измеряемой величины у.

III.ПРИБОРЫ ФИЗИЧЕСКОГО ПРАКТИКУМА.