Теоретические основы параметрических методов обработки экспериментальных данных (Раздел 2 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 8

Как видно из рисунка, состояниям E₁ и E₂ соответствуют некоторые подмножества значений переменной , попадание в которые результата наблюдения с наибольшей вероятностью соответствует тому или иному состоянию объекта. Поэтому, фиксируя попадание наблюдаемого результата в одно или другое подмножество, можно судить с некоторой вероятностью о состоянии, которое принял объект. Пусть такими подмножествами являются (–¥; x_a) и [x_a; +¥). Величина x_a является границей данных подмножеств. Тогда при x Î [x_a; –¥) принимается решение о нахождении объекта в состоянии E₁, а если x Î [x_a; ¥) – о нахождении объекта в состоянии E₂.

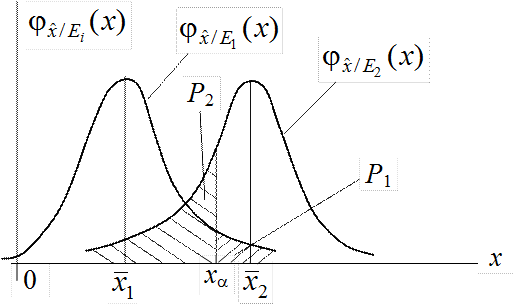
Рис.2.1. Условные законы распределения случайной величины

Поскольку кривые частично перекрываются, существует вероятность ошибки. Так, результат наблюдения с вероятностью

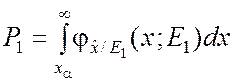                                                               (2.3.5)

может попасть в область [x_a; +¥), если объект находится в состоянии E₁, но при этом будет принято решение, что он пребывает в состоянии E₂. Это означает ошибку первого рода. Наоборот, с вероятностью

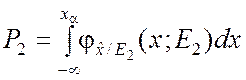                                                             (2.3.6)

результат наблюдения может попасть в область (–¥; x_a), если объект находится в состоянии E₂, но принимается решение о пребывании объекта в состоянии E₁. Будет допущена ошибка второго рода.

Если последствия ошибочных решений оценить невозможно, то очевидно, что решающее правило должно обеспечивать минимум суммы вероятностей (2.3.5) и (2.3.6). Так как данное правило состоит в определении границы x_a, она должна выбираться таким образом, чтобы минимизировать величину

                               .

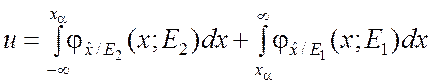Общих правил выбора оптимального значения x_a не существует. На практике чаще всего минимизируется вероятность ошибки первого рода до определённой заранее назначенной величины. На основе этого и выбирается значение критической границы.

В том случае, когда объект может находиться более чем в двух состояниях, применение рассмотренного принципа существенно усложняется. Ввиду этого используется не сам наблюдаемый параметр, а построенная на его основе специальная функция, так называемый показатель согласованности (см. раздел 7).

Следует отметить, что на основе рассмотренных выше принципов  может быть сформировано большое число показателей и критериев принятия решений, специфика построения которых определяется особенностями конкретной задачи.

2.4. Элементы теории оценивания

Первичной задачей обработки экспериментальных данных является задача оценивания. При её решении наибольшее распространение получил принцип максимального правдоподобия и вытекающие из него критерии и алгоритмы оценивания.

Пусть схема наблюдения имеет вид

                                                   ,                      (2.4.1)

а вектор ошибок измерений  имеет нормальное распределение

                                       ,

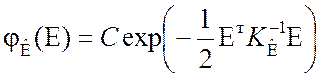где  – нормирующий множитель;  – корреляционная матрица вектора ошибок измерений.

Учитывая, что

                                                   ,

плотность распределения  можно выразить через  и F(A):

                      .

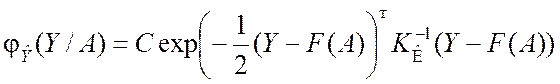Тогда принцип максимального правдоподобия приводит к следующей функции потерь:

                                .   (2.4.2)

Таким образом, при нормальном законе распределения выборки функция потерь является квадратичной. В частном случае, когда все элементы выборки имеют одинаковое распределение с дисперсией s² и независимы, функция  потерь  (2.4.2)  принимает вид

                                   .      (2.4.3)

Метод оценивания, основанный на минимизации квадратичной функции потерь вида (2.4.2) или (2.4.3), называется методом наименьших квадратов (см. раздел 8). Этот метод является оптимальным и для ряда других распределений ошибок наблюдений.

Если рассматривать схему наблюдения (2.4.1) в предположении, что вектор ошибок измерений имеет распределение Лапласа, то получим функцию потерь в виде суммы модулей ошибок. Метод оценивания вектора параметров, основанный на минимизации функции потерь как суммы модулей ошибок измерений, называется методом наименьших модулей  [8].

В настоящей брошюре он не рассматривается. Следует только отметить, что данный метод является оптимальным и в ряде других задач оценивания.