Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

Окончательно получаем выражение для вычисления оценок искомых параметров:

                                  .   (9.2.20)

Рассмотренный выше метод определения оценок коэффициентов регрессии без каких-либо изменений применим и в модели РА-2. Однако при этом необходимо учитывать то обстоятельство, что в модели РА-1 зависимость между  и x является односторонней. При рассмотрении же модели РА-2 исследователь сталкивается со взаимностью зависимости между  и . Поэтому в последнем случае правомерна формулировка задач двух типов.

1. Исследование зависимости  от  и построение уравнения регрессии  на :

                                                  .

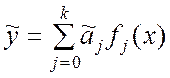2. Исследование зависимости  на  и построение уравнения регрессии  на :

                                                  ,

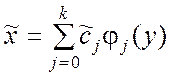где  – оценки коэффициентов регрессии.

9.2.3. Проверка адекватности уравнения регрессии

Под адекватностью  уравнения регрессии понимается соответствие данного уравнения экспериментальным данным.

Адекватность уравнения определяется, прежде всего, правильным выбором класса Y функций регрессии.

Для проверки соответствия выбранного класса функций регрессии опытным данным рассмотрим очевидное тождество

                                , . (9.2.21)

Возведём обе части (9.2.21) в квадрат и найдём для них математические ожидания:

                                                                          

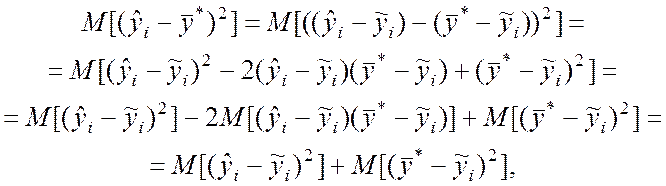
так как

                      .  

В результате получим

                              

или

                                                    ,                    (9.2.22)

где s² – общая дисперсия результатов наблюдений (дисперсия выходной переменной),  – дисперсия, характеризующая рассеивание результатов наблюдений относительно регрессионной зависимости (остаточная дисперсия);  – дисперсия, характеризующая отклонение регрессионной зависимости относительно истинной.

Чем меньше рассеивание результатов относительно регрессионной зависимости, тем лучше последняя аппроксимирует истинную (но неизвестную) зависимость (удовлетворяет экспериментальным данным). Таким образом, чем больше отношение , тем более адекватно уравнение регрессии. Поэтому выражение

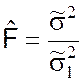                                                        ,                         (9.2.23)

принимается в качестве показателя согласованности при проверке нулевой гипотезы H₀ о соответствии выбранного класса функций регрессии экспериментальным данным. В связи с тем, что случайная величина (9.2.23) подчиняется закону распределения Фишера [1], критерием правильности гипотезы H₀ является выполнение неравенства

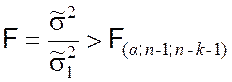                                              ,              (9.2.24)

где F – наблюдаемое (вычисленное) значение показателя согласованности гипотезы H₀;  – критическое значение данного показателя при уровне значимости a и степенях свободы    f₁ = n – 1,   f₂ = n – k – 1. Критическое значение берётся по таблице критических точек распределения Фишера (приложение 5). Входами в таблицу являются величины  a,  f₁,   f₂.

Оценки дисперсий  и  находятся по формулам:

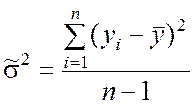                                                ;                 (9.2.25)

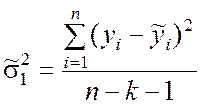                                                .                (9.2.26)

В случае невыполнения условия (9.2.24) принимается конкурирующая гипотеза H₁, т.е. возникает проблема выбора другого класса функций регрессии, более точно соответствующего экспериментальным данным. Проверка неравенства (9.2.24) называется проверкой адекватности уравнения регрессии по критерию Фишера.

9.2.4. Проверка значимости коэффициентов регрессии

Важным аспектом качества регрессионной зависимости является значимость коэффициентов регрессии a_j, . Поскольку оценки этих коэффициентов получены на основе случайной выборки, возникает задача проверки того, что их величина определяется именно видом  зависимости между  и x, а не случайным характером выборки. Эта задача сводится к проверке гипотез о неравенстве нулю коэффициентов a_j: