Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 11

Учитывая, что  = 1, окончательно получаем

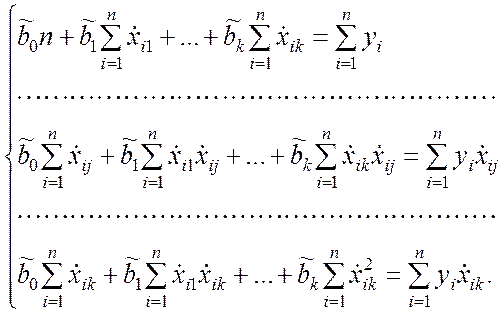                                                                                   (9.3.13)

Система (9.3.13) является системой линейных уравнений относительно оценок коэффициентов регрессии . Данные оценки находим по формулам Крамера:

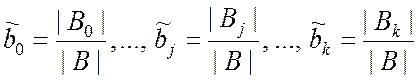                                , (9.3.14)

где | B | – определитель коэффициентов при неизвестных системы уравнений (9.3.13);    | B_j |,  – определители, полученные из определителя | B | заменой  j-го  столбца столбцом свободных членов.

Развёрнутый вид данных определителей:

; ;                                                                                                                     

;                                 .

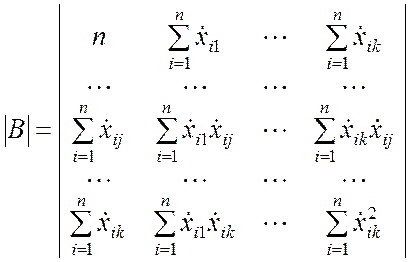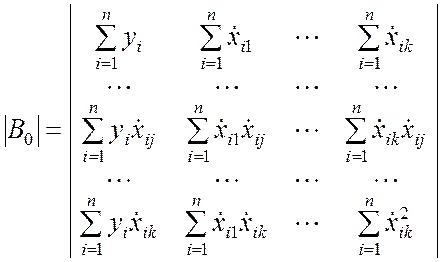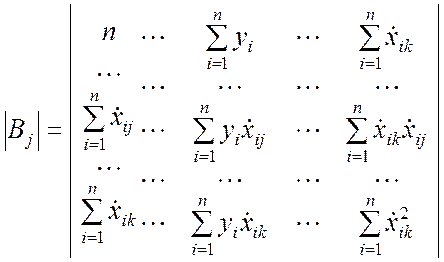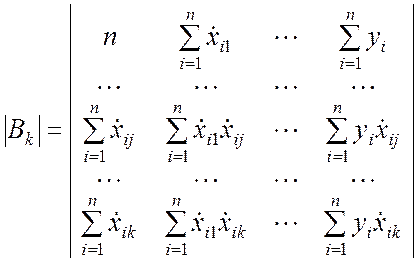Система уравнений (9.2.13) может быть записана в виде матричного уравнения

                                 ,  (9.3.15)

где                                     ,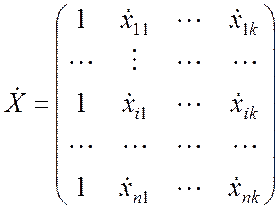

                              ;   .

Для получения вектора  умножаем обе части матричного уравнения (9.3.15) на  слева:

                                   ,

отсюда

                                              

или

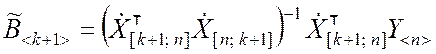                               ,                                                        (9.3.16)

где E = E_[k+1] – единичная матрица порядка (k+1).

Рассмотренный метод построения уравнения регрессии применим как для модели РА-1, так и РА-2.

9.3.3. Проверка адекватности уравнения множественной         регрессии

Подобно однофакторному регрессионному анализу, проверка адекватности экспериментальным данным уравнения множественной регрессии производится на основании анализа отношения дисперсий. В качестве показателя согласованности нулевой гипотезы H₀ об адекватности уравнения принимается выражение, аналогичное выражению (9.2.23):

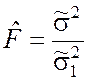                                                        ,                         (9.3.17)

где  – оценка общей дисперсии наблюдаемой переменной;  – оценка остаточной дисперсии.

Оценки дисперсий, входящих в соотношение (9.3.17), определяются по формулам

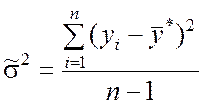                                                ,                (9.3.18)

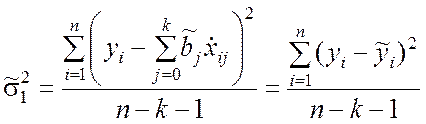                                , (9.3.19)

где – оценка математического ожидания наблюдаемой переменной;      n –1 – число степеней свободы дисперсии s²;  n – k –1 – число степеней свободы  дисперсии  .

Случайная величина (9.3.17) подчинена закону распределения Фишера [1]. Следовательно, для принятия нулевой гипотезы необходимо и достаточно, чтобы выполнялось условие

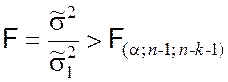                                              ,               (9.3.20)

где F –наблюдаемое значение показателя согласованности гипотезы H₀;  – критическое значение данного показателя при уровне значимости a и степенях свободы   f₁ = n –1,   f₂ = n – k –1.  Критическое значение показателя берётся по таблице критических точек распределения Фишера (приложение 5).

При невыполнении условия (9.3.20) принимается конкурирующая гипотеза H₁ о том, что линейная модель (9.3.1) или (9.3.2) неадекватна экспериментальным данным.

9.3.4. Селекция факторов

Уравнение регрессии связывает наблюдаемую переменную с совокупностью k факторов. Можно предположить (выдвинуть гипотезу), что какая-то часть этих факторов не оказывает существенного влияния на величину переменной y. Такие факторы без ущерба для точности могут быть исключены из уравнения. Возникает задача выявления таких факторов. Значимость любого фактора определяется, прежде всего, величиной коэффициента регрессии при данном факторе. Следовательно, задача селекции факторов сводится к проверке значимости коэффициентов регрессии. Такая задача решалась в однофакторном регрессионного анализе (пп. 9.2.4).

Следуя представленной в указанном подпараграфе схеме, необходимо проверить нулевые гипотезы о неравенстве нулю коэффициентов b_j:

                                              H_0j: b_j ¹ 0,   .