Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике), страница 8

   Так как отношение – это частный случай соответствия, то для него действительны все известные способы задания соответствий, в частности графический и матричный. Но так как области отправления и прибытия здесь совпадают, то имеются некоторые особенности. Например, при матричном способе задания матрица всегда получается квадратной. При графическом способе задания области отправления и прибытия изображаются одним множеством точек.

Пример 1.18.

   Рассмотрим отношение из примера 1.17. Матрица этого отношения будет иметь вид:

		1	2	3	4	5	6
M(R) =	1	1	1	1	1	1	1
	2	0	1	0	1	0	1
	3	0	0	1	0	0	1
	4	0	0	0	1	0	0
	5	0	0	0	0	1	0
	6	0	0	0	0	0	1

   Графическое представление:

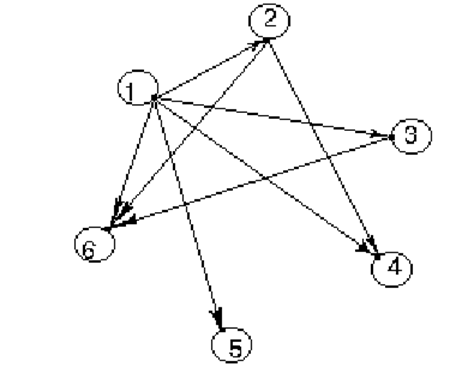
   Так как каждое число делится на себя, то это изображается петлей в соответствующей точке (на петле стрелку можно не ставить).

1.4.5.3. Операции над отношениями

   Над отношениями можно выполнять все операции, которые выполняются над соответствиями. При этом, естественно, нужно учитывать особенности определения и задания отношений. Так, композиция возможна только для отношений, заданных на одном и том же множестве. Если композиция выполняется графически, то оба отношения изображаются на одном и том же множестве элементов (точек), причем стрелки, относящиеся к разным отношениям, обозначаются по-разному (например, для первого отношения – сплошными линиями, для второго – пунктирными). В композицию включаются такие пары элементов, которые соединены путями из двух стрелок, первая из которых принадлежит первому отношению, а вторая – второму.

Пример 1.19.

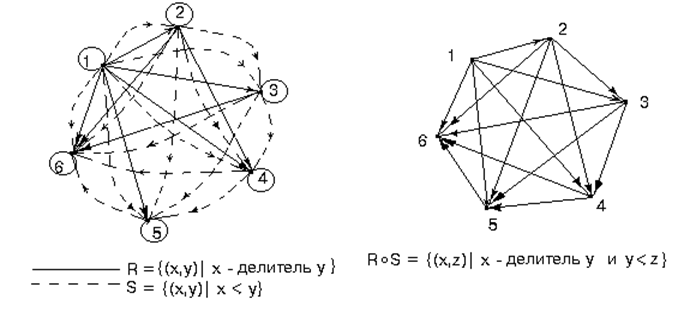
   Кроме того, имеется специфическая операция, называемая транзитивным замыканием отношения.

   Если R – отношение на множестве Х: R Í Х´Х, то его транзитивное замыкание обозначается , причем оно задано на том же множестве Х, т.е. и пара (x, y) Î R тогда и только тогда, когда существует цепочка элементов
z₀=x, z₁, ..., z_n=y, такая, что

                                                                                  ___

z_i-1Rz_i, i=1, n,

то есть любая пара идущих друг за другом элементов этой цепочки входит в состав отношения R.

   Свойства транзитивного замыкания:

   1) Если (x, y) Î R, то , т.е. .

   2)  

(Ú читается "или"), откуда следует, что

т.е. транзитивное замыкание отношения R есть объединение всех степеней этого отношения, где под n-ой степенью отношения понимается композиция этого отношения с самим собой, выполненная n раз.

   Отсюда следует способ нахождения транзитивного замыкания графическим методом: строится графическое представление отношения; на нем ищутся всевозможные пути произвольной длины; в транзитивное замыкание включаются все те и только те пары элементов множества, первый из которых является началом пути, а второй его концом.

Пример 1.20.

   Пусть Х - множество людей. Определим отношение R следующим

образом:

                          R = {(x, y) | x – ребенок y)},

тогда транзитивным замыканием этого отношения будет

 = {(x, y) | x - потомок y)}

Пример 1.21.

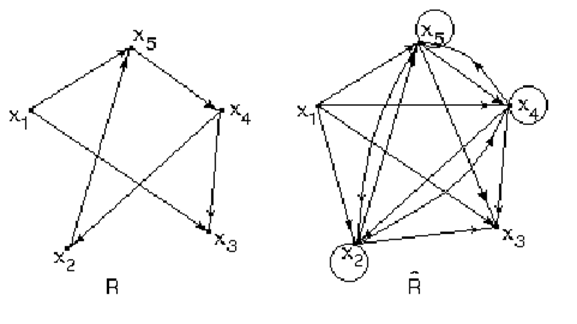
Пример 1.22.

   Отношение делимости из примеров 1.17, 1.18.

   Нетрудно видеть, что транзитивное замыкание этого отношения

совпадает с самим отношением.

1.4.2.4. Свойства отношений

   Ниже рассмотрены некоторые свойства, которыми могут обладать

отношения.

1) Рефлексивность

   Отношение R на множестве Х называется рефлексивным, если "х (х, х)ÎR, т.е. пары, состоящие из одинаковых элементов, всегда входят в отношение.

   В матрице рефлексивного отношения на главной диагонали всегда стоят только единицы. В графическом представлении рефлексивного отношения в каждой точке, изображающей объект из множества Х, имеется петля.