Дискретная математика: Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике), страница 12

   При матричном способе представления графов матрица композиции обычных графов получается как булево произведение матриц смежности исходных графов (см. композицию отношений), а матрица смежности композиции мультиграфов получается как обычное произведение матриц смежности исходных мультиграфов.

Задание. Выполните операции из предыдущего примера матричным способом и сравните полученные результаты с графическими.

2.3. Частичные графы и подграфы

   Граф H = (X, D) называется частичным графом для графа G = (X, Г), если они заданы на одном и том же множестве вершин и множество ребер графа H является подмножеством множества ребер графа G, т.е. D Í Г.

   Граф G_A = (A, Г_A) называется подграфом графа G = (X, Г), если А ÍХ, а множество его ребер состоит из всех тех ребер графа G, оба конца которых лежат во множестве А.

Пример 2.8.

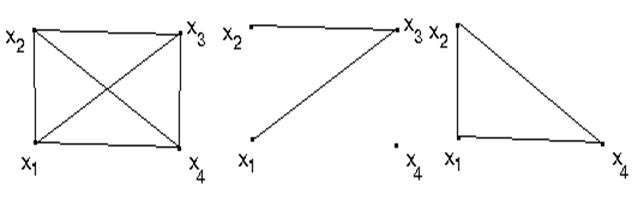
                        G = (X, Г)           H = (X, D)                   G_A = (A, Г_A)

2.4. Связность

2.4.1. Определения

   Пусть G(X) - неограф.

   Говорят, что вершины x_i и x_j связаны, если существует цепь S(x_i, x_j), соединяющая эти вершины.

   Граф G(X) называется связным, если любая пара его вершин связана.

   Отношение связности на графе рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности. Это отношение позволяет разбить множество вершин графа Х на классы Х_i так, что все вершины, входящие в один и тот же класс связаны между собой, а вершины из разных классов между собой не связаны.

   Подграф G(Х_i) графа G(X) называется связной компонентой графа G(X).

   Объединение всех связных компонент графа совпадает с самим графом, пересечение разных связных компонент одного и того же графа пусто.

   Пусть G(Х, Г) - орграф. Он связен, если связен соотнесенный неограф, получающийся из графа G(Х,Г) заменой всех его дуг звеньями.

   Орграф G(Х, Г) называется сильно связным, если для любых двух его вершин x_i и x_j (i ¹ j) существует путь из вершины x_i в вершину x_j.

   Сильно связный граф всегда связен. Обратное утверждение в общем случае неверно.

Пример 2.9.

   На следующем рисунке граф G₁ сильно связен и связен, граф G₂ связен, но не сильно связен.

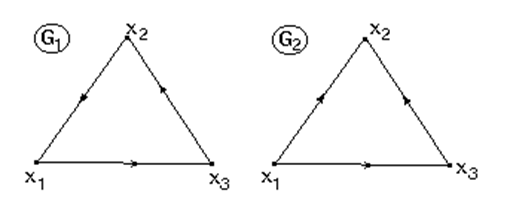
   Сильно связный подграф G' графа G называется максимальным сильно связным подграфом, если не существует другого сильно связного подграфа, строго содержащего в себе G'.

2.4.2. Алгоритм выделения максимальных сильно связных подграфов (алгоритм Мальгранжа)

   Введем следующие обозначения:

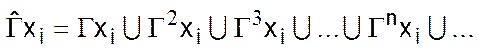
– множество вершин графа, достижимых из вершины x_i каким-либо путем (множество достижимости вершины x_i).

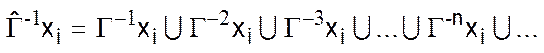
– множество вершин графа, из которых можно попасть в вершину x_i каким-либо путем (множество обратной достижимости вершины x_i).

С(x_i) - множество вершин максимального сильно связного подграфа, содержащего вершину x_i.

   В соответствии с определением максимального сильно связного подграфа С(x_i) содержит саму вершину x_i и множество вершин, в которые можно попасть из вершины x_i и вернуться обратно. Последнее множество представляет собой пересечение множеств достижимости и обратной достижимости вершины x_i. Таким образом,

   Множества  легко найти по матрице смежности графа. Для этого справа от матрицы смежности строят столбец, в котором указывается расстояние от выбранной вершины до всех остальных вершин графа. Вершины, которые нельзя достичь из выбранной вершины, помечаются крестиком (х). Около самой выбранной вершины в столбце ставится 0. Множество вершин, которым в этом столбце соответствуют цифры, образуют множество достижимости выбранной вершины.

   Затем под матрицей строят строку, в которой выписываются расстояния до выбранной вершины из всех остальных вершин. Вершины, из которых нельзя попасть в выбранную вершину, помечают крестиком. Выбранной вершине ставится в соответствие 0. Множество вершин, которым в построенной строке соответствуют цифры, представляет собой множество обратной достижимости выбранной вершины.

   Затем по формуле (2.1) находят множество вершин максимального сильно связного подграфа, содержащего выбранную вершину. Если нужно найти все максимальные сильно связные подграфы данного графа, то из матрицы смежности вычеркивают строки и столбцы, соответствующие найденному максимальному сильно связному подграфу и повторяют описанные выше действия. Эта процедура повторяется до тех пор, пока в матрице больше не останется элементов.