Символический
метод даёт те же результаты, но проще. Пусть ![]() . Тогда
. Тогда
![]() . Теперь
. Теперь ![]() есть
индуктивное сопротивление идеального элемента, величина чисто мнимая, что и
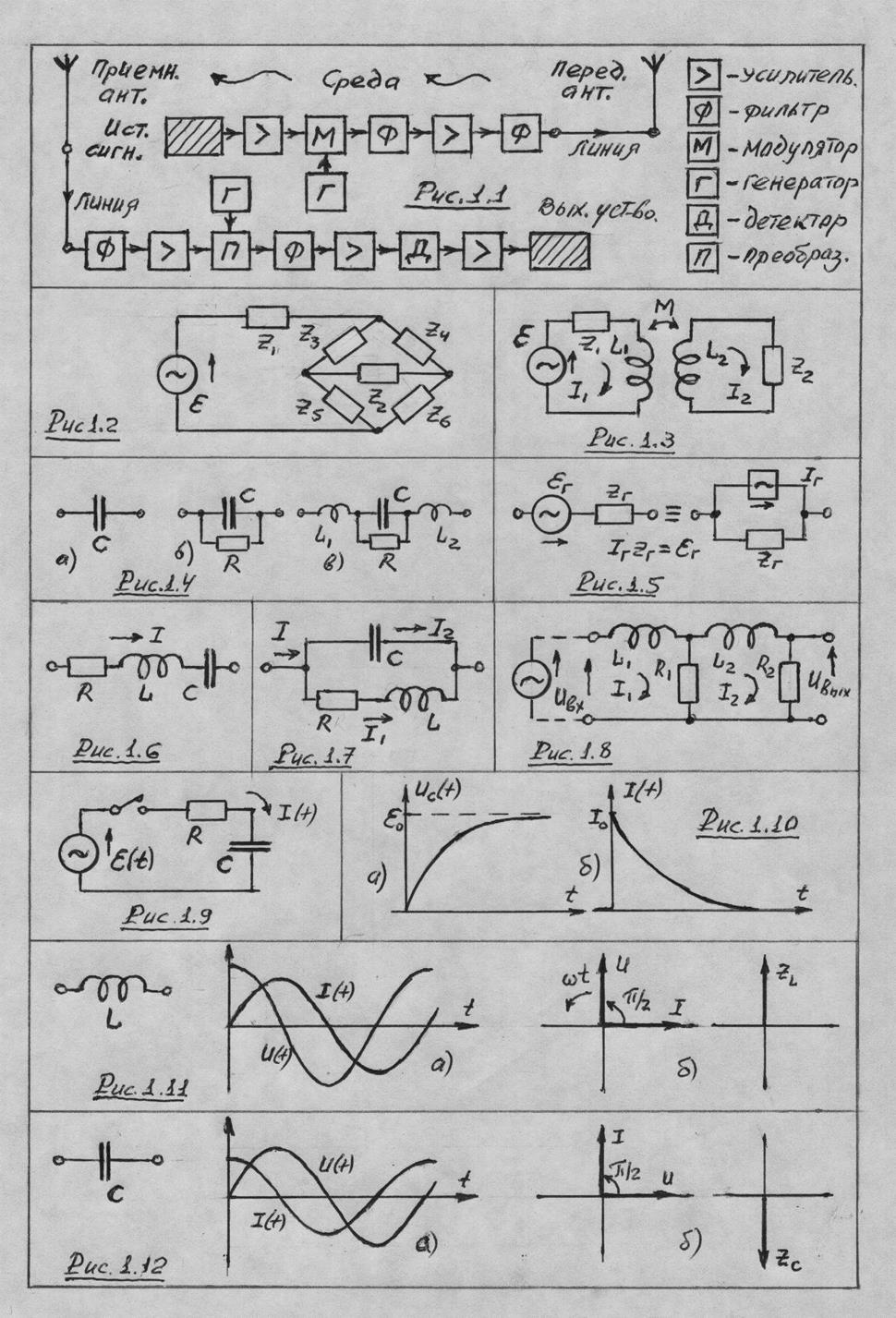
отражает его реактивность. Векторные диаграммы изображены на рис. 1.11б.
есть
индуктивное сопротивление идеального элемента, величина чисто мнимая, что и
отражает его реактивность. Векторные диаграммы изображены на рис. 1.11б.
в).
Идеальный ёмкостной элемент. Воспользуемся сразу символическим методом. Пусть ![]() . Тогда
. Тогда ![]() .
Ёмкостное сопротивление
.
Ёмкостное сопротивление ![]() .
. ![]() . Теперь ток опережает напряжение на
четверть периода. Средняя мощность опять равна нулю. Соответствующие картинки
изображены на рис. 1.12.
. Теперь ток опережает напряжение на
четверть периода. Средняя мощность опять равна нулю. Соответствующие картинки
изображены на рис. 1.12.
1.11. Некоторые обобщения и выводы.
Мы убедились в
том, что линейные задачи теории цепей, как и многие линейные физические задачи,
сводятся к решению линейного дифференциального уравнения с постоянными
коэффициентами порядка n. ![]() . Общее решение уравнения есть
сумма решений однородного уравнения
. Общее решение уравнения есть
сумма решений однородного уравнения ![]() и частного решения
исходного неоднородного
и частного решения
исходного неоднородного ![]() . Решение
однородного уравнения имеет такой типичный вид:
. Решение
однородного уравнения имеет такой типичный вид: 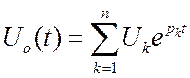 , где Uk есть постоянные
интегрирования (находятся из граничных условий), а pk - корни характеристического
уравнения (не кратные). При этом для систем с потерями (любая реальная цепь)
, где Uk есть постоянные
интегрирования (находятся из граничных условий), а pk - корни характеристического
уравнения (не кратные). При этом для систем с потерями (любая реальная цепь) ![]() для всех корней. Поэтому решение
однородного уравнения
для всех корней. Поэтому решение
однородного уравнения ![]() при
при ![]() . Эта часть решения описывает
"собственный" переходной процесс, присущий данной цепи.
. Эта часть решения описывает
"собственный" переходной процесс, присущий данной цепи.
Решение
неоднородного уравнения с постоянными коэффициентами имеет вид правой части.
Так, если ![]() , то
, то ![]() (
(![]() ), где Pmи
), где Pmи ![]() m полиномы. В
частности, когда
m полиномы. В
частности, когда ![]() , то
, то ![]() .
.
Частное решение
неоднородного уравнения называют "вынужденным" решением. Оно
описывает процесс, навязанный определенным сигналом f(t). Проблема
состоит в том, что многообразие реальных сигналов вынуждает нас каждый раз
заново решать дифференциальное уравнение для каждого нового сигнала. Можно
этого избежать? Для линейных цепей можно. В физике и теории цепей используют
стандартные, "пробные" функции для описания источников. Это, прежде
всего гармоническая функция ![]() (
(![]() или
или ![]() ) и дельта функция
-
) и дельта функция
- ![]() . Важно понять, почему именно эти функции используются.
. Важно понять, почему именно эти функции используются.
Гармоническая
функция ![]() является "характеристической",
особой для линейных цепей (для линейных дифференциальных уравнений с постоянными коэффициентами),
поскольку она воспроизводится цепью. Решение (напряжения и токи) меняется по
тому же закону
является "характеристической",
особой для линейных цепей (для линейных дифференциальных уравнений с постоянными коэффициентами),
поскольку она воспроизводится цепью. Решение (напряжения и токи) меняется по
тому же закону ![]() , с той же частотой. Надо найти
лишь амплитуду и фазу, два вещественных параметра или один комплексный, комплексную
амплитуду U0.
Дифференциальное уравнение при этом сводится к алгебраическому (проявляется
преимущество символического метода). Это одно обстоятельство.
, с той же частотой. Надо найти
лишь амплитуду и фазу, два вещественных параметра или один комплексный, комплексную
амплитуду U0.
Дифференциальное уравнение при этом сводится к алгебраическому (проявляется
преимущество символического метода). Это одно обстоятельство.
Однако главное состоит в том, что, зная реакцию цепи на гармонические сигналы различных частот (всех), мы можем найти реакцию цепи на любое другое воздействие, уже не решая больше уравнение. Всё сводится к интегрированию. Надо вычислить интеграл Фурье.
Функция ![]() представляет сосредоточенное,
"точечное" возбуждение, пространственное или временное. Решение
уравнения
представляет сосредоточенное,
"точечное" возбуждение, пространственное или временное. Решение
уравнения ![]() в физике называют функцией Грина, ввиду
особой роли этого решения. Зная функцию Грина g(t), мы можем сразу
написать решение дифференциального уравнения для любого другого воздействия f(t). Алгоритм получения
решения очень простой. Всё сводится к вычислению свертки функций f(t) и g(t).
в физике называют функцией Грина, ввиду
особой роли этого решения. Зная функцию Грина g(t), мы можем сразу
написать решение дифференциального уравнения для любого другого воздействия f(t). Алгоритм получения
решения очень простой. Всё сводится к вычислению свертки функций f(t) и g(t). 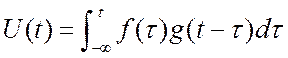 . При этом нам уже не надо больше решать
уравнение. Вся необходимая информация о системе содержится в функции g(t).
. При этом нам уже не надо больше решать
уравнение. Вся необходимая информация о системе содержится в функции g(t).
Таким образом,
основная идея метода анализа линейных цепей такова. Сложный сигнал
представляется суперпозицией некоторых стандартных (например, ![]() , d (t) и др.).
Находится реакция цепи на эти отдельные сигналы. Потом всё суммируется
(интегрируется).
, d (t) и др.).
Находится реакция цепи на эти отдельные сигналы. Потом всё суммируется
(интегрируется).
Для нелинейных цепей это не годится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.