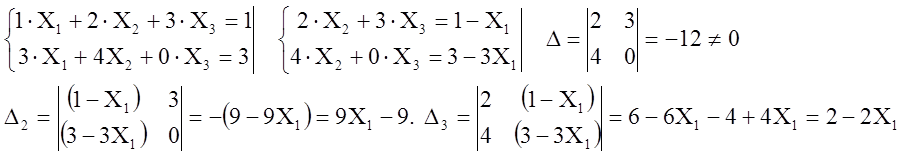
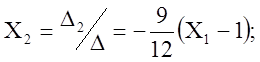
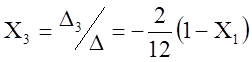 ;
;
Отв. ![]()
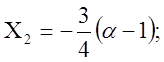
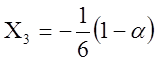
![]()
![]()
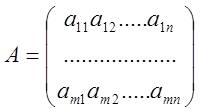
![]() .
.
Определение Число
строк и число столбцов матрицы А называют ее структурой и обозначают ![]()
а) ![]() квадратная
матрица. Для нее определения понятие определителя
квадратная
матрица. Для нее определения понятие определителя ![]() . Если
определитель квадратной матрицы не равен нулю, то такая матрица называется невырожденной,
и вырожденной в противном случае.
. Если
определитель квадратной матрицы не равен нулю, то такая матрица называется невырожденной,
и вырожденной в противном случае.![]()
б) ![]() вектор строки.
вектор строки.![]()
в) ![]() вектор столбца.
вектор столбца.
Определение Две матрицы А и В называются равными, если они имеют одинаковую структуру
![]()
![]() и
состоят из соответственно равных элементов.
и
состоят из соответственно равных элементов.
![]() (1).
(1).
Определение Суммой
двух матриц А и В, имеющих одинаковую структуру, называется матица С, имеющая
такую же структуру, с элементами ![]() , равными суммам
соответствующих
, равными суммам
соответствующих
элементов матриц слагаемых.
![]()
![]()
![]() (2).
(2).
Пример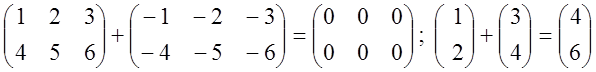
Особую роль при сложении играет нулевая матрица 0:
Определение Матрица все элементы которой равны нулю, называются нулевой.
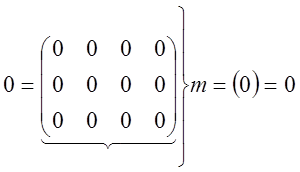
Нулевая матрица, будучи сложенной с произвольной
матрицей, не изменяет эту матрицу. ![]()
Свойство. Операция сложения матриц обладает коммутативности и ассоциативности.
![]()
Определение Произведением
матрицы А на число ![]() называют матрицу В той же
структуры, что и матрица А с элементами, равными произведению соответствующих
элементов матрицы А на число
называют матрицу В той же
структуры, что и матрица А с элементами, равными произведению соответствующих
элементов матрицы А на число ![]() .
.
![]()
![]() (3)
(3)
Теорема. Если определитель квадратной матрицы А равен ∆, то определитель матрицы В=aА будет равным an×∆, где n- порядок матрицы А.
Опр. Операция вычитания матриц А и В определяется как операция сложения матрицы А с предварительно умноженной на a= -1 матрицей В, т.е.
![]() (4)
(4)
Опр. ![]()
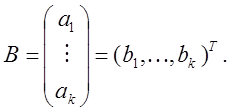 Произведением вектор-строки А на
вектор-столбец В называют число, равное сумме парных произведений соответствующих
элементов А и В.
Произведением вектор-строки А на
вектор-столбец В называют число, равное сумме парных произведений соответствующих
элементов А и В.
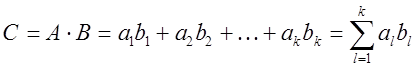
Опр. Произведением матрицы А размера ![]() на матрицу В размера
на матрицу В размера
![]() называют матрицу С
размера
называют матрицу С
размера ![]() , элемент Сij
которой равен произведению i-строки
матрицы А на j-столбец матрицы В, т.е.
, элемент Сij
которой равен произведению i-строки
матрицы А на j-столбец матрицы В, т.е.
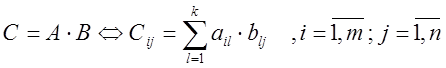 (5)
(5)
Из определения следует:
1) Умножать можно только такие матрицы, у которых число столбцов первой матрицы равно числу строк во второй.
2) Число строк результирующей матрицы С равно числу строк первой матрицы сомножителя А, а число столбцов равно числу столбцов второго сомножителя В.
Свойства: Произведение квадратных матриц ассоциативно, дистрибутивно, но не
коммутативно, т.е. ![]() /ассоц./
/ассоц./
![]() /дистриб./
/дистриб./
![]() ; /в общем случае не
коммутативно./
; /в общем случае не
коммутативно./
Пример.
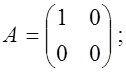
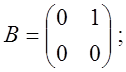
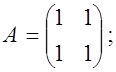
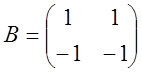
![]()
![]() но А¹0; В¹0;
но А¹0; В¹0;
Особую роль при умножении матриц играет единичная матрица Е.
Опр. Единичной матрицей называют квадратную матрицу, у которой элементы, расположенные на главной диагонали, равны 1, а все остальные элементы 0.
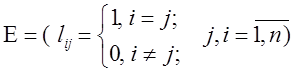
Свойства: Умножение матрицы А с матрицей Е не изменяют матрицу А:
![]()
Если матрица А квадратная, то АЕ=ЕА=А.
Теорема (об определителе произведения квадратных матриц ).
Если А и В – две квадратные матрицы
одного порядка с определителями /А/ и /В/, то определитель произведения АВ
равен произведению определителей /А/×/В/ т.е., ![]() (6)
(6)
Доказательство:
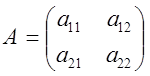 ;
; 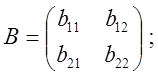
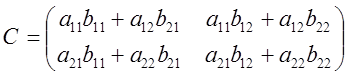
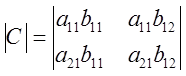 +
+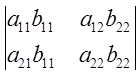 +
+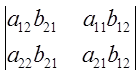 +
+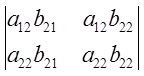 =
=
= 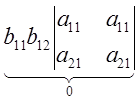 +
+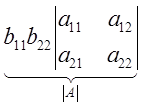 +
+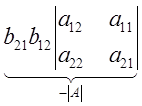 +
+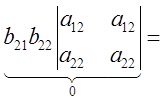
=![]() .
.
Определение
Квадратная матрица ![]() называется обратной по отношению
к квадратной матрице А, если
называется обратной по отношению
к квадратной матрице А, если ![]() (7)
(7)
Теорема. (о существовании обратной матрицы )
Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной.
Доказательство: Необходимость. Пусть матрица А
имеет обратную ![]() . Покажем, что в этом случае
. Покажем, что в этом случае ![]() . Если допустить противное, т.е.,
. Если допустить противное, т.е., ![]() ,
,
![]()
![]() , что невозможно, а значит
, что невозможно, а значит ![]() .
.
Достаточность. Пусть ![]() .
Покажем (найти обратную).
.
Покажем (найти обратную).
Алгоритм построения обратной матрицы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.