В урне пять шаров разного размера. Какова вероятность вытянуть все шары по возрастанию, если известно, что одинаковых шаров нет?
Решение. Общее число
возможных элементарных исходов опыта равно числу перестановок из пяти элементов
![]() , а число исходов, благоприятствующих
событию, равно единице.
, а число исходов, благоприятствующих
событию, равно единице.
Искомая вероятность:
 .
.
Набирая номер телефона, абонент забыл последние две цифры, и помня что они различны, набрал их на удачу. Какова вероятность того, что он набрал нужный номер?
Решение. Общее число
возможных исходов опыта равно числу размещений из 10 по 2, т. е. ![]() . Число исходов, благоприятствующих
событию, равно единице.
. Число исходов, благоприятствующих
событию, равно единице.
Искомая вероятность:
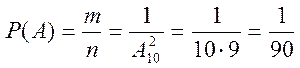 .
.
В ящике стола имеется 15 тетрадей, 8 из них в клеточку .Наудачу взяли три тетради. Найти вероятность того, что все три взятые тетради окажутся высшего качества.
Решение. Так как порядок
здесь роли не играет, то общее число всевозможных исходов будет равно числу
сочетаний из 15 по 3, т. е. ![]() , а число
благоприятствующих событию равно тоже числу сочетаний из 8 по 3.
, а число
благоприятствующих событию равно тоже числу сочетаний из 8 по 3.
Искомая вероятность:
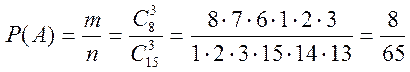 .
.
В группе 15 студентов, 8 из которых отличники. Наудачу ( по списку ) вызвали 6 студентов. Найти вероятность того, что 4 студента из вызванных окажутся отличниками.
Решение. Число всевозможных
исходов опыта здесь равно числу сочетаний из 15 по 6, ![]() .
.
Благоприятной считаем такую
комбинацию, в которой 4 студента-отличника, а 2 - нет. 4 отличника можно
выбрать из 8 отличников ![]() способами, при
этом остальные 6-4=2 студента (не отличники) выбираем из 15-8=7 студентов
способами, при
этом остальные 6-4=2 студента (не отличники) выбираем из 15-8=7 студентов ![]() способами.
способами.
Если к каждой четверке
отличников присоединить одну из ![]() пар
пар
студентов, не отличников, то получим
“благоприятные” группы из 6 человек. Их число равно m =![]()
![]() .
.
Искомая вероятность:
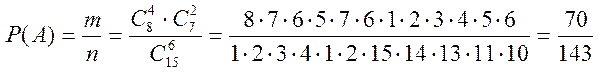 .
.
Первая трудность, которую преодолел Паскаль в своей переписке с шевалье де Маре, связана с точным подсчетом случаев. Речь шла об игре, при которой бросают три кости, и один из игроков заключает пари, что сумма на выброшенных гранях будет больше чем 10, а другой - что она будет равна или меньше 10. Легко видеть, что шансы обоих игроков равны. Но трудность была в следующем. Терпеливый учет очень большого числа партий показал шевалье де Маре, что тот кто ставит на сумму, большую 10, чаще выигрывает с 11,чем с12 очками. Однако, возражал Мере,11 очков можно получить шестью различными способами ( 6-4-1; 6-3-2; 5-5-1; 5-4-2; 5-3-3; 4-4-3 ), и 12 очков тоже можно получить шестью способами ( 6-5-1; 6-4-2; 6-3-3; 5-5-2; 5-4-3; 4-4-4). Ответ Паскаля очень прост: сочетание 6-4-1 не является простым, а шестикратным, так как, если пронумеровать кости или если каждую из трех костей окрасить по разному, чтобы можно было их различить, значение 6 может быть получено на каждой из трех костей, а значение 4 - на каждой из двух остающихся, что уже составляет шесть комбинаций. Напротив, такое сочетание, как 5-5-1, может быть получено только тремя различными способами, а сочетание 4-4-4 - единственным способом.
Следовательно, если желательно узнать действительное число различных способов получить 11 или получить 12 очков, то надо для каждого из этих случаев составлять сумму тех шести чисел, которые соответствуют сочетаниям,
6+6+3+6+3+3=27,
тогда как для случая 12 очков мы имеем
6+6+3+3+6+1=25.
Отсюда заключаем, что в среднем мы получаем 11 очков 27 раз, тогда как 12 очков мы получаем 25 раз, и этот результат отлично сошелся с наблюдениями шевалье де Мере.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.