Аппроксимация кривой намагничивания методом гиперболического синуса

                                                             

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

Расчетно-графическая работа

По дисциплине:                               Материаловедение.                                                                                 

(наименование учебной дисциплины согласно учебному плану)

Тема: Аппроксимация кривой намагничивания методом гиперболического синуса и методом степенного ряда.

Выполнил: студент  гр. АПМ-03     ______________    /Никифоров М.Н./

                                                                                                     ^{(подпись)                                  (Ф.И.О.)}  

ПРОВЕРИЛ:

Руководитель:                                     ____________         /Анискин Б.Г./

                                                                                                      ^{(подпись)                                (Ф.И.О.)}

Санкт-Петербург                                 

2005 год.

Задача 1. Аппроксимация кривой методом гиперболического синуса.

Исходные данные.

Исходные данные заданы в виде зависимости (табличная форма).

Вариант 10.

H, А/см	В, Тл	Марка стали	Толщина листа, мм
10	1,3	Э 41	0,5
25	1,46
50	1,57
100	1,7
300	1,9

Ход работы.

Кривая намагничивания задана точками. Построим кривую №1. Выглядит она следующим образом:

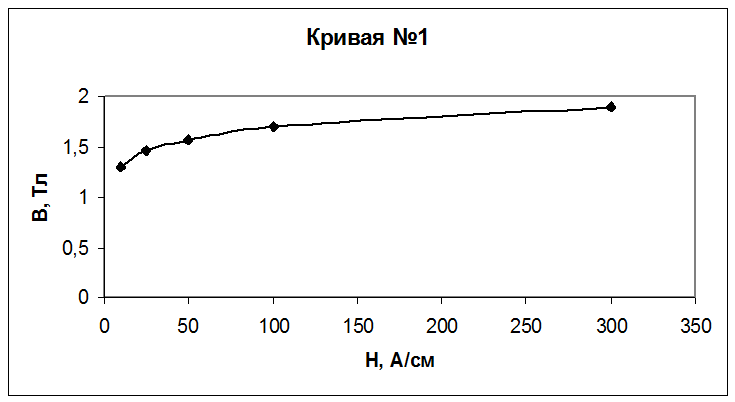
            Аппроксимация кривой методом гиперболического синуса осуществляется с использованием формулы

                                                                                                                           (1)

где  и  - коэффициенты. На кривой №1 берем две произвольные точки с координатами  и , например: ,  и ,  соответственно. Подставим эти значения в уравнение (1) и поделим одно уравнение на другое, получим:

=;

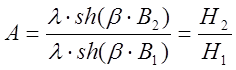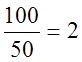            Для определения величины коэффициента  зададим произвольные значения , большие и меньшие А, при известных  и  и найдем ряд значений  и . По этим значениям получим зависимость  и в осях  и  найдем значение  для известного А. Сделаем вспомогательную табличку:

	0,5	1	1,5	4	7	10
	1,101333856	1,150624191	1,218877262	1,682031466	2,484322534	3,669296668

            Построим график зависимости , получим:

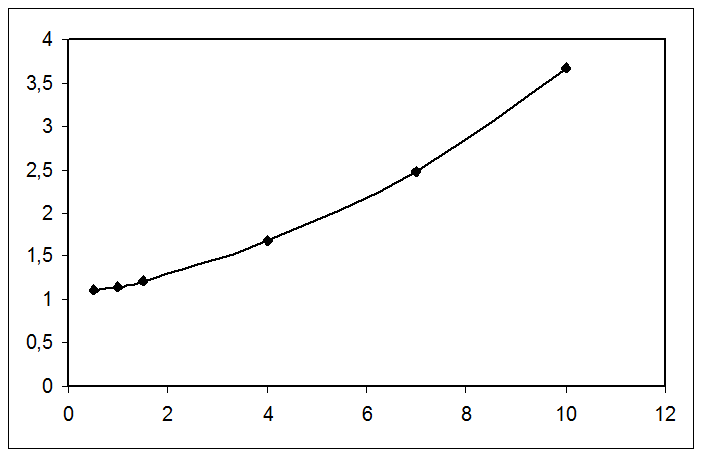
Для значения А=2, находим экспериментальным путем значение . Получим .

Определим коэффициент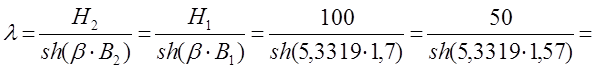

.

            После определения коэффициентов  и  построим таблицу значений кривой №2 с помощью формулы (1), задаваясь значениями В, тех же осях, что и кривая №1:

Построив график кривой по данным таблицы, получим кривую №2, которую изобразим вместе с кривой №1, как это показано ниже.

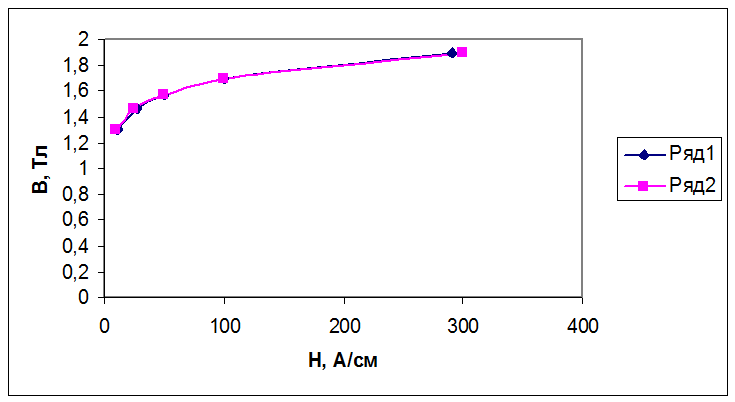
            Для определения ошибки аппроксимации кривой №1 необходимо для заданных значений В определить ошибку .

                                                                                                                              (2),

где значения напряженности магнитного поля кривой №1, значения напряженности магнитного поля кривой №2. Все значения  возводим в квадрат, получим: =101,9957526;

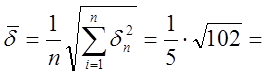2,019858931.

Вывод по задаче №1.

Аппроксимировав данную кривую намагничивания методом гиперболического синуса, можно увидеть, что аппроксимация оказалась успешной, что видно и из рисунка и по значению ошибки .

Задача №2. Аппроксимация кривой намагничивания методом степенного ряда.

Ход работы.

            Исходные данные те же, что и в задаче №1. Кривая 3 строится с использованием формулы

                                                                                                                   (4),

при тех же значениях В, что и в первой задаче. Для каждого значения В определяем ошибку :

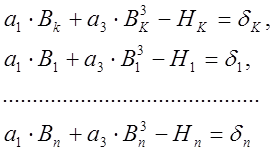                                                                                                        (5).

            Левые и правые части уравнений (5) возведем в квадрат, затем сложим почленно. Получим:

               (6).

Найдём производные по  и , получим:

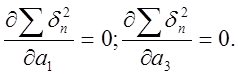
Далее:

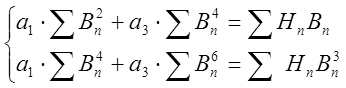                                                                                            (7).

Подставив данные кривой №1 и подсчитав суммы получим:

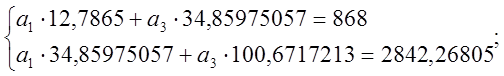
Откуда

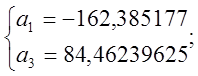
Подставив найденные значения  и  в уравнение (6), найдем величину , получим:

            По формуле 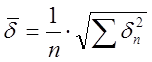получим .

            При известных  и  по уравнению (4), подставляя значения В, получим ряд значений Н. Занесем из в следующую таблицу:

            Построив график кривой по данным таблицы, получим кривую №3, которую изобразим для наглядности вместе с кривой №1 и кривой №2, как это показано ниже.

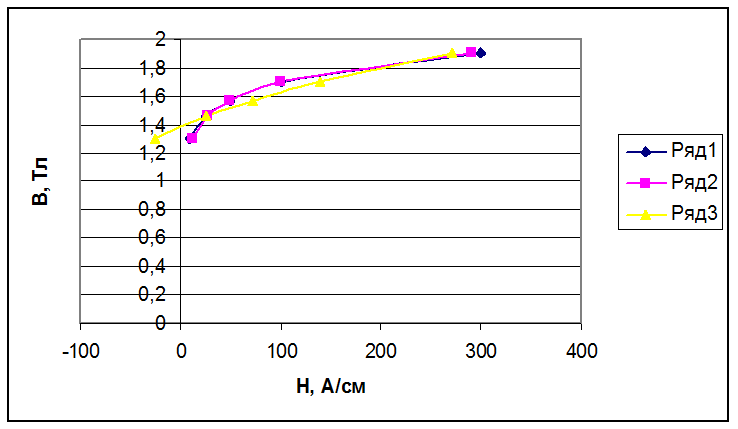
Вывод по задачам №1 и №2.

Аппроксимировав данную кривую намагничивания методом степенного ряда (методом наименьших квадратов), можно увидеть, что аппроксимация оказалась наиболее успешной при применении аппроксимации при помощи метода гиперболического синуса, в котором , в отличие от аппроксимации методом степенных квадратов, в котором .