Степенные ряды, страница 4

Начнем исследование с ряда (2). Этот ряд необходимо сравнить с обобщенным гармоническим рядом при  т.е.   который сходится. Здесь можно применить как обычный признак сравнения, так и предельный. Сравним члены ряда (2) и члены эталонного ряда:

Следовательно, по признаку сравнения из сходимости ряда с большими членами вытекает сходимость ряда с меньшими членами, т.е. степенной ряд в точке  сходится.

Чтобы исследовать ряд (1), заметим, что его ряд из модулей совпадает с рядом (2), а следовательно, сходится, что позволяет утверждать, что  знакочередующийся ряд (1) сходится абсолютно.

Таким образом, область сходимости степенного ряда имеет вид:

            Пример. Найти область сходимости ряда  

Находим радиус сходимости степенного ряда:

Следовательно, при  степенной ряд сходится абсолютно, а при  ряд расходится. Неисследованными остались две точки  и  Выпишем числовые ряды, которые возникают при подстановке этих точек:

(1)       и   (2)  

Начнем с ряда (2), он знакоположительный и его можно исследовать с помощью предельного признака сравнения. В качестве  эталонного рассмотрим  гармонический ряд  

Т.к. предел отношения членов исследуемого ряда и эталонного равен 1, по предельному признаку сравнения ряды ведут себя одинаково. Гармонический ряд расходится, следовательно, и ряд (2) тоже расходится.

            Теперь рассмотрим знакочередующийся  ряд (1), для него расходящийся ряд (2) является рядом из модулей, следовательно, ряд (1) не сходится абсолютно. Чтобы проверить сходится ли он вообще, воспользуемся признаком Лейбница.

            1) Необходимое условие сходимости: 

            2) монотонное убывание абсолютных величин членов ряда: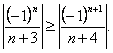  

Таким образом, условия признака Лейбница выполнены, следовательно, ряд (1) сходится. Но мы уже знаем, что абсолютной сходимости нет, т.е. сходится он условно.

Область сходимости степенного ряда имеет вид:

            Определение. Будем говорить, что степенной ряд  сходится к функции  на интервале  и писать  если для любой точки   выполнено равенство

            Пример. Найти сумму ряда  

Выше было показано, что область сходимости этого ряда  и при каждом  из области сходимости возникает геометрический ряд. Для геометрического ряда известно, что   Таким образом,