Степенные ряды, страница 3

            Теорема о радиусе сходимости степенного ряда. Если, начиная с некоторого номера  все коэффициенты  степенного ряда  отличны от нуля, то радиус сходимости ряда может быть найден как предел отношения абсолютных величин коэффициентов:

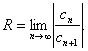
Доказательство. Для исследуемого степенного ряда  выпишем ряд из модулей  и исследуем его для каждого фиксированного значения  по признаку Даламбера. Рассмотрим предел

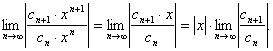
Согласно признаку Даламбера знакоположителный числовой ряд сходится, если предел отношения его последующего члена к предыдущему меньше единицы, т.е.

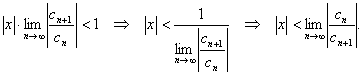
Мы получили условие, при котором сходится ряд из модулей членов степенного ряда, следовательно, сам степенной ряд при этих же условиях сходится абсолютно. С другой стороны, по признаку Даламбера ряд расходится, если тот же предел больше единицы, что в нашем случае дает условие: 

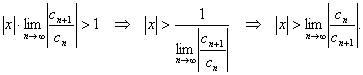
Мы уже обсуждали, что у рядов, которые по признаку Даламбера расходятся, на самом деле, невыполнено необходимое условие сходимости, и этот факт позволяет утверждать, что мы получили условие, при котором расходится не только ряд из модулей степенного ряда, но и сам степенной ряд. Таким образом, мы нашли число 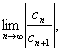 удовлетворяющее определению радиуса сходимости степенного ряда. Ч.т.д.

Пример. Найти область сходимости ряда  

Начинать решение такой задачи следует с отыскания радиуса сходимости ряда по теореме о радиусе сходимости степенного ряда.

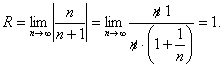
Следовательно, при  степенной ряд сходится абсолютно, а при  ряд расходится. Неисследованными остались две точки  и  Выпишем числовые ряды, которые возникают при подстановке этих точек:

(1)                и         (2)    

Мы получили хорошо знакомые нам ряды, они расходятся, поскольку для них не выполнено необходимое условие сходимости.

            Таким образом, область сходимости степенного ряда имеет вид:

Пример. Найти область сходимости ряда  

Находим радиус сходимости степенного ряда:

Следовательно, при  степенной ряд сходится абсолютно, а при  ряд расходится. Неисследованными остались две точки  и  Выпишем числовые ряды, которые возникают при подстановке этих точек:

(1)       и   (2)  

Обратите внимание на особенность этих рядов:  ряд (2) является рядом из модулей для ряда (1). Так всегда связаны числовые ряды, возникающие при подстановке    и   поэтому при исследовании начинать удобно со знакопостоянного ряда, а потом результат использовать для знакопеременного ряда.