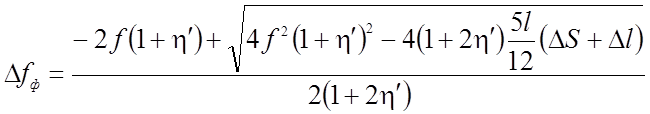Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 1, страница 4

         (2.17)

Заметим, что для жестких нитей, используемых в висячих покрытиях, двучлен под корнем всегда будет положительным, причем первый член под корнем во много раз больше второго. Это дает основание подкоренное выражение в формуле разложить в степенной ряд. Тогда выражение для определения фиктивного прогиба примет вид:

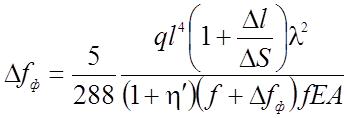                                                              ( 2.18 )

Для нити, имеющей формулу кубической параболы без шарнира в середине пролета (рис. 2.16) формула для определения фиктивного прогиба остается без изменения, меняется только коэффициент h'.

Рассматривая полученные решения, видим, что для нити, имеющей формулу кубической параболы, фиктивный прогиб зависит прямо пропорционально от удлинения нити и подвижности опор, обратно пропорционален величине начального провеса.

Большое влияние на фиктивный прогиб оказывает жесткость на растяжение EA, чем она больше, тем при прочих равных условиях меньше прогиб и связанные с ним изгибные явления.

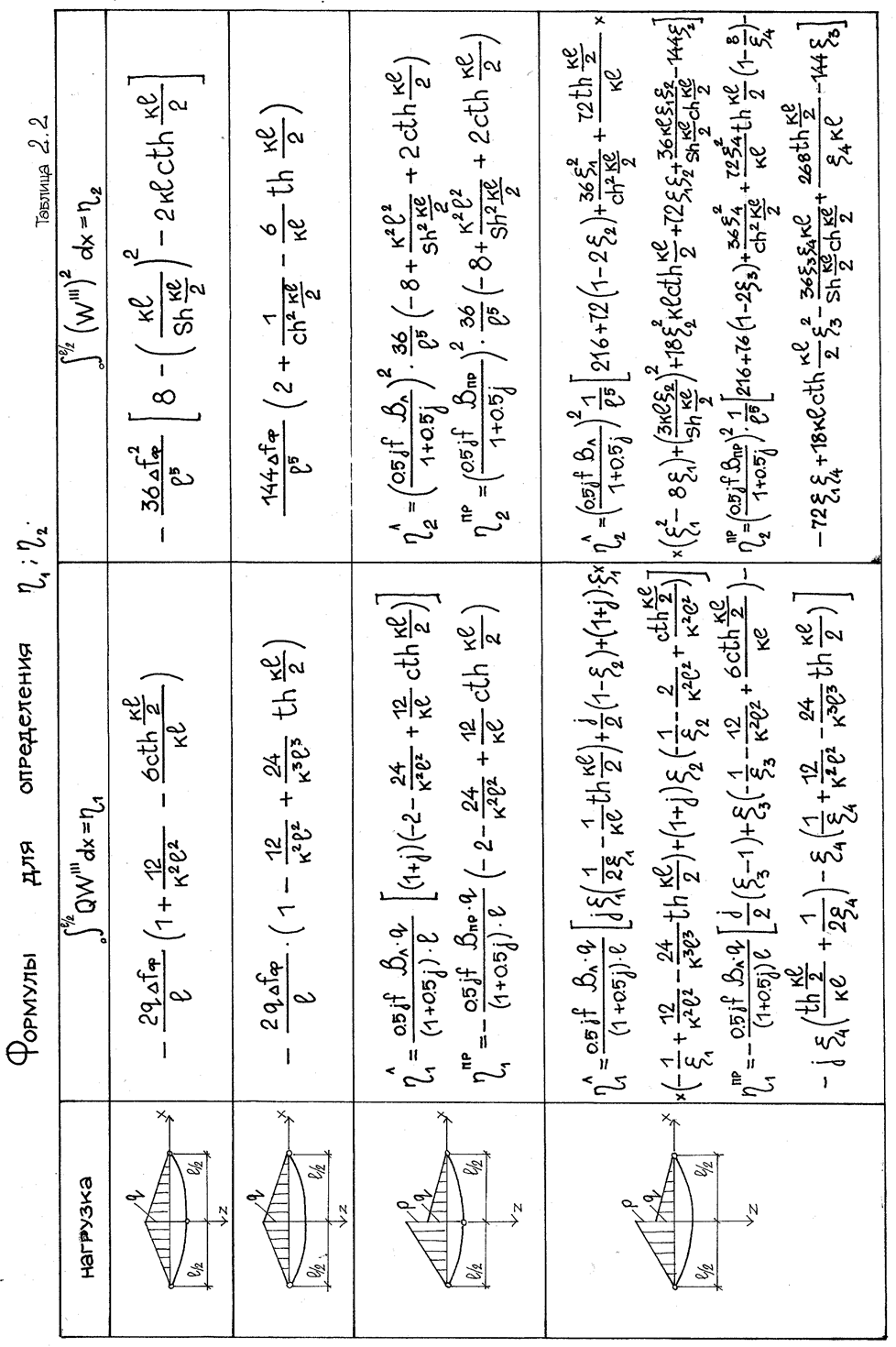
Для того, чтобы оценить влияние изгибной жесткости на прогибы и его производные, построим графики для различных значений Kl (рис.2.3). При построении графиков величинами малых порядков будем пренебрегать. Анализируя полученные графики видим, что изгибная жесткость нити при равновесной нагрузке мало влияет на прогибы (коэффициент h' не превышает значение 0,15 - 0,2). Максимальное значение прогиба находится в середине пролета.

Зная вторую производную от прогиба, можно определить момент, изгибающий нить, по формуле:

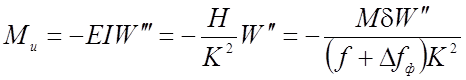                                          ( 2.19 )

Во всех случаях вторая производная, а, соответственно, и изгибающий момент нарастают от опоры к середине, затем резко падают до нуля в нити, имеющий в середине пролета шарнир. Для нити, имеющей шарниры только на опоре, изгибающий момент достигает максимума в середине пролета. Изгибающие моменты от полной нагрузки, вообще говоря, невелики и не превосходят величины

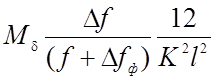
Анализируя формулы, замечаем, что чем больше гибкость, тем меньше величина момента, тем больше его максимум смещается к середине пролета у нити, имеющей в центре шарнир. Подставляя вместо W" ее значение, а также считая 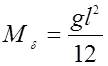, получаем для трёхшарнирной нити

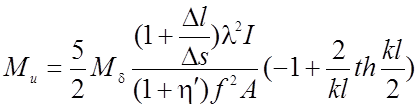                                                   (2.20)

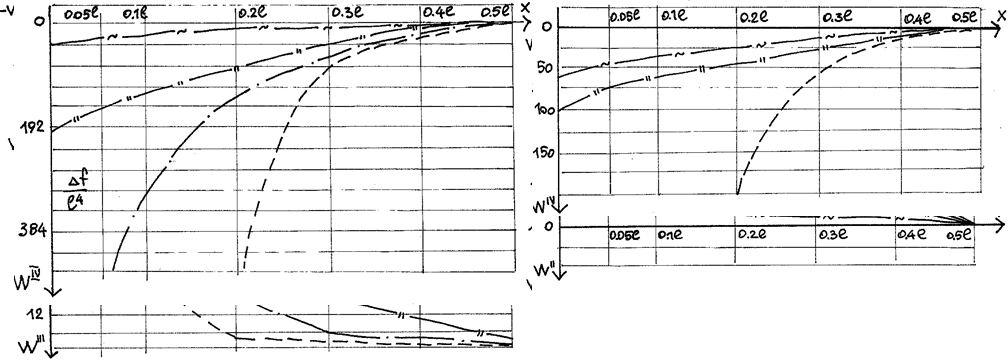
Рис.2.3. Эпюры прогибов и его производных

Для нити, имеющей шарниры только на опоре, максимальный изгибающий момент определяется по формуле:

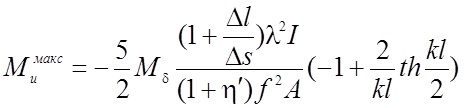                                             (2.21)

Из (2.20, 2.21) видно, что полный момент распределяется между "балкой" и нитью пропорционально изгибной жесткости нити (EI) и произведению f²A, играющему роль условного момента инерции. Для симметричного сечения высотой h напряжения определяются по формуле 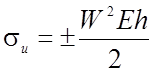. В частном случае для нити изображённой на рис.2.1 имеем :

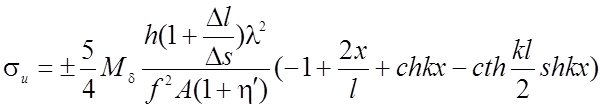                         (2.22)

Из формулы 2.22 видно, что напряжение обратно пропорционально начальной стрелке f², прямо пропорционально высоте сечения h и зависит от смещения опор и жёсткости нити.

Перевязывающая сила находится из условия Q_u = -EIW".

Для трехшарнирной жесткой нити

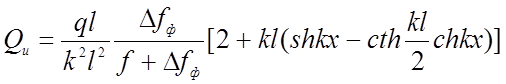                                       (2.23)

Отношение 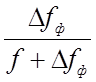показывает, что величина перерезывающей силы незначительна.

Условная нагрузка q_и , которая изгибает нить, как видно из графиков, мала. Для нити, изображенной на рис.2.1, она достигает максимума в середине пролета равного 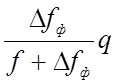 , а затем быстро уменьшается к опорам.

На основе приведенных выше рассуждений устанавливаем, что при равновесной нагрузке изгибная жесткость нити несущественно влияет на ее работу и не эта нагрузка является определяющей при назначении изгибной жесткости.