Теоретические исследования работы жестких нитей в двухполюсной радиально-вантовой системе. Часть 1, страница 3

Выражение (2.10) является квадратным уравнением относительно стрелки деформированной кривой тяжения. Решая его относительно Df_ф , получим .

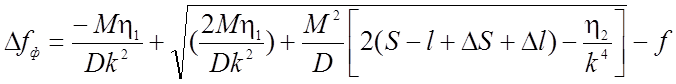
Вынося за скобки Mh₁/Dk², имеем

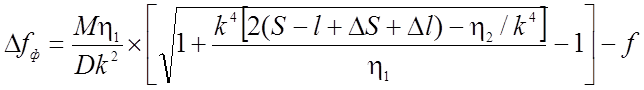                      (2.11)

Если второй член под корнем меньше единицы, то от корня можно освободиться. Тогда выражение (2.11) с небольшой погрешностью можно записать

 

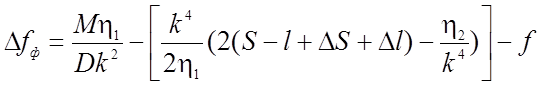
Формула рекуррентна, поскольку значение h₁ и h₂ содержат третью производную w". Она уточняется последовательным приближением.

2. Расчет жестких нитей, изогнутых на кубической параболе.

В двухполюсной радиально-вантовой системе нити расходятся из двух противоположных углов. По мере удаления от угла, расстояние между нитями возрастает и, если нагрузка равномерно распределена на площади покрытия, то погонная нагрузка, действующая на нить, увеличивается прямо пропорционально расстоянию. Для такой нагрузки эпюра изгибающих моментов соответствует выражению

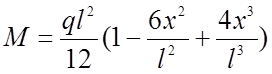                                                                    (2.12)

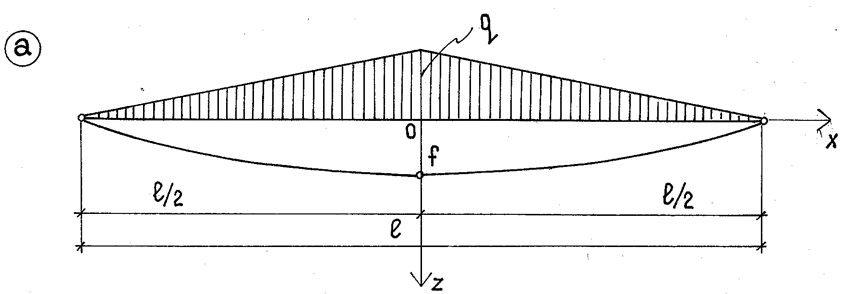
Равновесной будем считать такую нагрузку, эпюра изгибающих  моментов которой повторяет очертание нити. Если рассматривать гибкую нить, то любая нагрузка заставляет ее принять очертание эпюры моментов, но так как она обладает изгибной жесткостью, сопротивляется этим изменениям. Поэтому, чем больше исходное очертание нити будет отличаться от эпюры моментов, тем большая сила будет заставлять ее принять эту форму, тем большие изгибающие моменты будут в ней возникать. Для того, чтобы при полной расчетной нагрузке изгибающие моменты в жесткой нити были малы, она должна иметь начальное очертание, повторяющее эпюру моментов от этой нагрузки. Рассматриваемая нить, имеющая начальную стрелку f, должна иметь ординаты, изменяющиеся по закону:

 

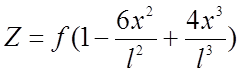
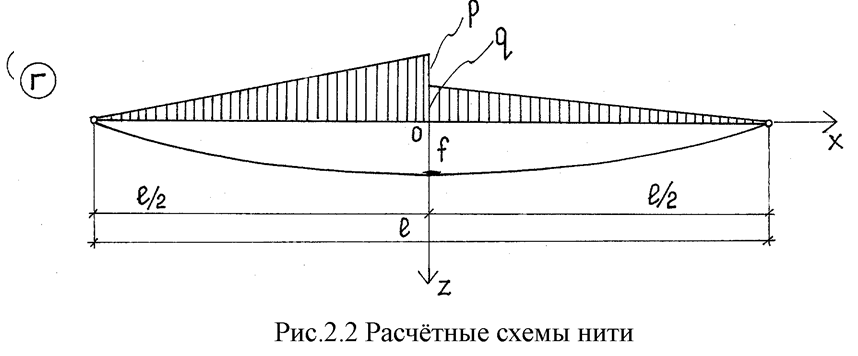
При выборе расчетной схемы следует обратить внимание на конструкцию узлов соединения нити с диагональной распоркой, которое может быть шарнирным или жестким. В работе рассматривается два вида нитей (рис.2.2а, 2.2.б). Для упрощения расчета систему координат помещаем в середину пролета и, используя симметрию, рассматриваем только правую половину пролета.

Для нити, изображенной на рис. 2.2а, решая уравнение (2.4), получаем:

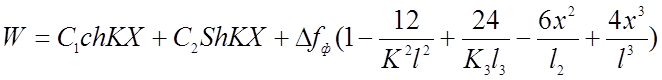                  (2.13)

Величины произвольных постоянных определяются из условий крепления нити для каждого частного случая загружения. Если нить имеет шарниры на обоих опорах и в центре , то постоянные C₁ и C₂ находятся из условий:

При 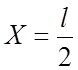        W=0, при X=0 W=Df_ф

Формула прогибов получает вид:

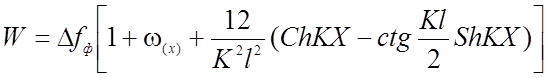                                   (2.14)

Здесь и в дальнейшем примем обозначение

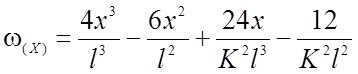
Необходимо отметить, что для данной нити фиктивный прогиб равен действительному, так как она имеет в центре шарнир.

Если нить имеет шарниры только на опорах (рис. 2.2б), то постоянные интегрирования находятся из условий:

при 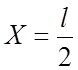  ®   W = 0 ,    При х = 0   ®  W' = 0

Решение имеет вид :

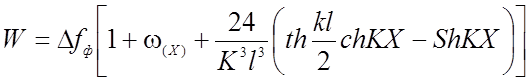                                    (2.15)

Для нахождения прогиба Df_ф в середине пролета используем формулу    (2.10) .

Заменим некоторые величины, входящие в формулу, значениями, которые они  имеют для данной нагрузки:

                        

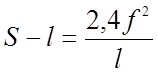
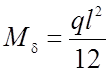
Значение h₁,h_2, D_r приведены в таблицах 2.1, 2.2. Тогда для вычисления фиктивного прогиба получим квадратное уравнение:

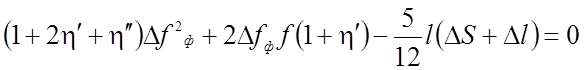                            (2.16)

где h' и  h" приведены в таблице 2.2

Сравнивая коэффициенты h'и h", замечаем , что h' на два, три порядка выше h", поэтому для практических вычислений можно  коэффициент h" положить равным нулю.

Решение квадратного уравнения дает: