При 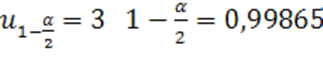 , откуда
, откуда ![]() , т.е. если согласны на ошибку в 3 случаях из 1000, то можем использовать «правило
, т.е. если согласны на ошибку в 3 случаях из 1000, то можем использовать «правило ![]() ».
».
Поскольку в (1.46') входит, как правило, заранее неизвестная
величина ![]() , то она заменяется несмещенной
статистической оценкой
, то она заменяется несмещенной
статистической оценкой ![]() , причем
, причем
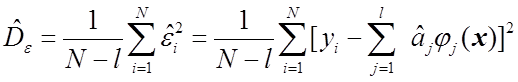
(1.50)
Из общих соотношений (1.46') можно получить формулы для одномерной
линейной модели ![]() , а именно:
, а именно:
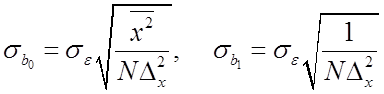 ,
(1.51)
,
(1.51)
где
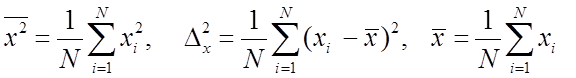 .
.
1.2) Интервальная оценка линейной регрессии 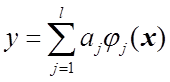 .
.
Учитывая, что ![]() и
и ![]() , получим
, получим
![]() , (1.52)
, (1.52)
а тогда дисперсия ![]() может быть рассчитана по формуле
может быть рассчитана по формуле
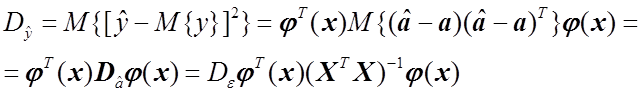 (1.53)
(1.53)
В частном случае, когда ![]() , можно получить
, можно получить
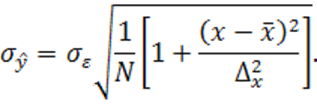
(1.54)
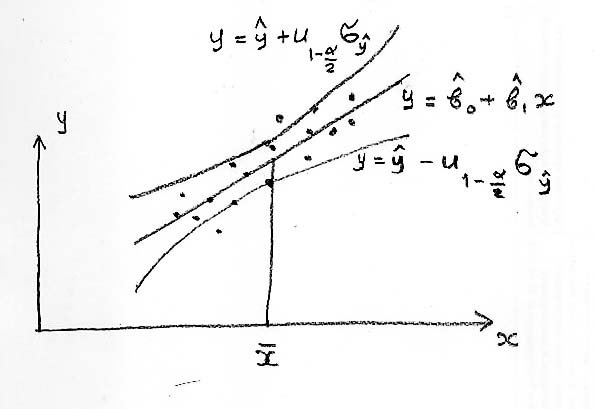
Границы доверительного интервала находятся аналогичным образом
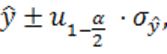
где при расчете ![]() по формуле (1.53) или (1.54) вместо
по формуле (1.53) или (1.54) вместо ![]() подставляется (1.50).
подставляется (1.50).
2) Малые выборки
2.1) Интервальные оценки параметров модели ![]() .
.
При формировании интервальных оценок приходится иметь дело со случайной величиной
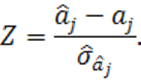
Зная распределение ![]() и задавшись надежностью оценок, т.е.
доверительной вероятностью
и задавшись надежностью оценок, т.е.
доверительной вероятностью ![]() , можно с помощью соотношений типа (1.47) – (1.49) определить доверительный интервал для оценок
, можно с помощью соотношений типа (1.47) – (1.49) определить доверительный интервал для оценок ![]() .
.
При большой выборке (ориентировочно ![]() )
оценка
)
оценка ![]() близка к константе
близка к константе ![]() , поэтому распределение
, поэтому распределение ![]() близко к нормальному. При малой выборке
распределение
близко к нормальному. При малой выборке
распределение ![]() существенно отличается от нормального, и
это должно учитываться при формировании интервальных оценок. Чтобы найти
распределение
существенно отличается от нормального, и
это должно учитываться при формировании интервальных оценок. Чтобы найти
распределение ![]() , рассмотрим предварительно два
вспомогательных, но широко используемых в статистике, типа случайных величин и
их распределений.
, рассмотрим предварительно два
вспомогательных, но широко используемых в статистике, типа случайных величин и
их распределений.
а) ![]() –распределение.
–распределение.
Пусть ![]() — независимые случайные величины со
стандартным нормальным распределением. Рассмотрим случайную величину
— независимые случайные величины со
стандартным нормальным распределением. Рассмотрим случайную величину
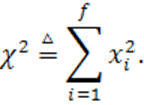 (1.55)
(1.55)
Тогда можно показать, что плотность вероятности случайной величины ![]() , называемая
, называемая ![]() –распределением с
–распределением с ![]() степенями свободы, имеет вид
степенями свободы, имеет вид
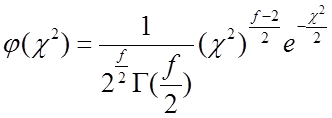 для. f > 1, (1.56)
для. f > 1, (1.56)
где 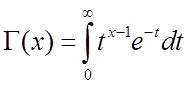 ,
причем
,
причем ![]() .
.
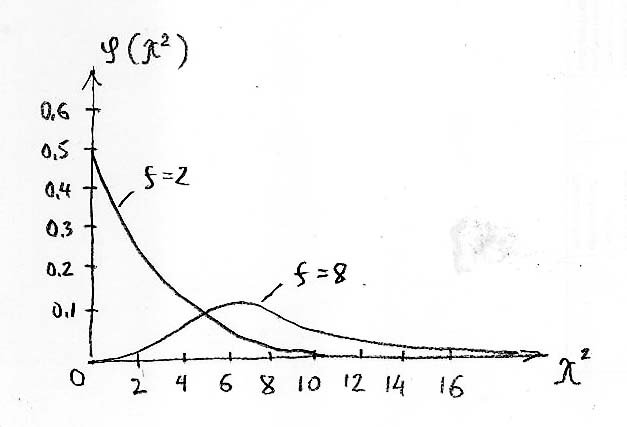
Кривая ![]() –распределения одновершинная, ассиметричная
и асимптотически приближается к оси абсцисс. С ростом
–распределения одновершинная, ассиметричная
и асимптотически приближается к оси абсцисс. С ростом ![]() вершина сдвигается вправо и
вершина сдвигается вправо и ![]() –распределение стремится к нормальному.
Поскольку
–распределение стремится к нормальному.
Поскольку 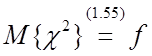 , то максимум в районе f.
, то максимум в районе f.
б) Распределение Стьюдента (псевдоним английского статистика
Госсета) или ![]() –распределение.
–распределение.
Пусть случайная величина ![]() имеет стандартное нормальное
распределение, т.е.
имеет стандартное нормальное
распределение, т.е. ![]() , а случайная величина
, а случайная величина ![]() —
— ![]() –распределение с
–распределение с ![]() степенями свободы, т.е.
степенями свободы, т.е. ![]() , причем
, причем ![]() и
и ![]() независимы. Тогда можно показать, что
плотность вероятности случайной величины
независимы. Тогда можно показать, что
плотность вероятности случайной величины
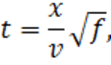 (1.57)
(1.57)
называемая распределением Стьюдента с ![]() степенями свободы, имеет вид
степенями свободы, имеет вид
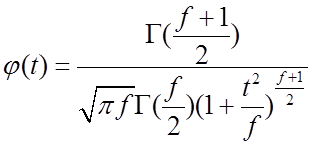 .
(1.58)
.
(1.58)
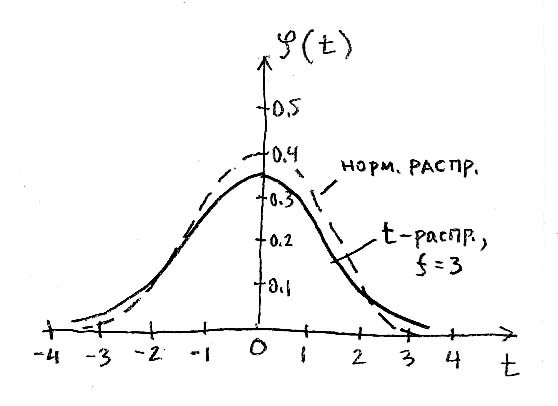
Функция ![]() четная. При малых
четная. При малых ![]() она более плоская, чем кривая стандартного
нормального распределения, но с ростом
она более плоская, чем кривая стандартного
нормального распределения, но с ростом ![]() приближается к распределению
приближается к распределению ![]() .
.
Распределению Стьюдента подчинено, например, отношение
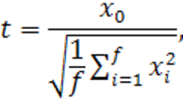
где ![]() ,
, ![]() , …,
, …, ![]() — взаимно независимые нормально
распределенные центрированные случайные величины с дисперсией
— взаимно независимые нормально
распределенные центрированные случайные величины с дисперсией ![]() .
.
Это становится очевидным, если представить ![]() в виде
в виде
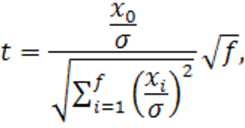
где
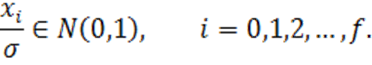
Возвращаясь к вопросу о распределении случайной величины
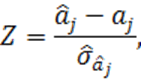
представим ее в виде
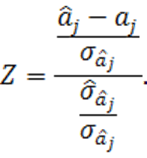
Ясно, что случайная величина в числителе подчиняется стандартному
нормальному распределению ![]() . С учетом (1.46') случайную величину в знаменателе можно записать в форме
. С учетом (1.46') случайную величину в знаменателе можно записать в форме
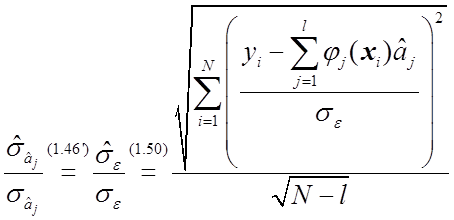 ,
,
а значит
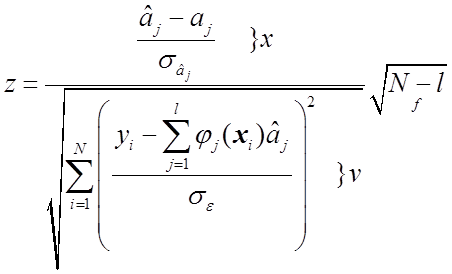
Можно доказать, что случайные величины в числителе и знаменателе ![]() и
и ![]() взаимно независимы, причем
взаимно независимы, причем ![]() , а
, а ![]() , а тогда
, а тогда ![]() .
.
Следовательно, выполняется соотношение
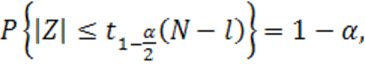
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.