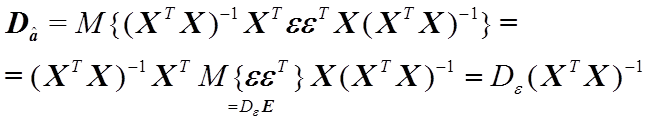Прикладные методы в теории вероятности, страница 6

.                (1.44)

Допустим, что . Тогда

                  .

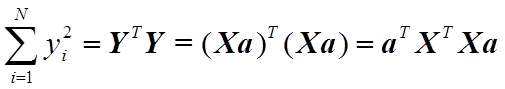С другой стороны,

                   

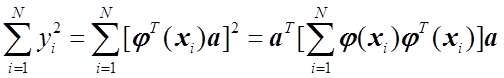
Сравнивая два полученных выражения, приходим к выводу, что

                                 .

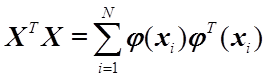                                                                                       (1.45)

Если допустить, что существует

                                

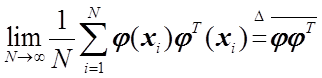
то

                          

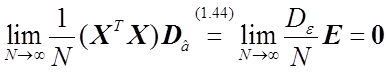
или

                                          ,

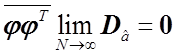откуда следует, что

                                                 .

Следовательно, с ростом объема выборки оценки МНК в среднеквадратическом сходятся к истинным значениям параметров регрессионной модели

3) Эффективность:

                                                   ,                                    (1.46)

где  — корреляционная матрица оценок a, найденных любым другим методом.

(Справка: для двух квадратных матриц A и B неравенство  означает, что для любого x выполняется условие .)

По поводу эффективности приведем два факта.

1) МНК оценки являются наилучшими в смысле (1.46) среди любых несмещенных оценок, полученных линейным преобразованием результатов измерений, т.е. оценок вида , причем это свойство не требует допущения о нормальном распределении измерительных ошибок  (доказательство смотри, например, в книге В. В. Федорова «Теория оптимального эксперимента»).

2) При условии нормальности распределения измерительных ошибок  МНК оценки являются эффективными в классе асимптотически нормальных оценок, т.е. удовлетворяют условию (1.46). Доказательством этого служит то, что при нормальности , как было показано раньше, МНК оценки совпадают с оценками ММП, которые обладают этим свойством.

1.5. Точность оценок метода наименьших квадратов

Для решения вопроса о точности модели следует указать доверительные интервалы для искомой регрессии 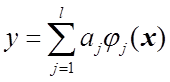 и коэффициентов .

В общем виде задача построения доверительного интервала формулируется следующим образом. Пусть по выборке из некоторой генеральной совокупности (т.е. множества всех возможных значений данных) определена оценка  некоторого параметра, точное (но неизвестное) значение которого равно . Поскольку  определяется по конечной выборке в условиях случайных измерительных помех, то эта оценка — случайная величина, значение которой, вообще говоря, может отличаться от .

Интересует интервал , в котором с достаточно высокой, так называемой, доверительной вероятностью  (на практике ) находятся истинные значения .

Рассмотрим вопрос о построении доверительных интервалов отдельно для больших  и малых  выборок (напомним, что N – размер выборки, а l – число оцениваемых параметров модели).

1) Большие выборки

1.1) Интервальные оценки параметров модели .

Ранее было показано, что при фиксированной выборке x оценки  имеют математическое ожидание  и корреляционную матрицу 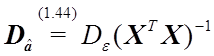. Введем обозначение . Тогда

                                       

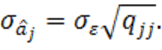
                                                                                      (1.46’)

Из (1.43), нормальности измерительных ошибок  и того факта, что линейная функция от нормально распределенных величин есть нормально распределенная случайная величина, следует, что

                                        

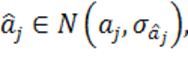
а тогда

                                    

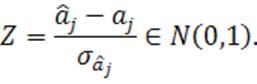
Известно, что для случайной величины

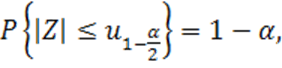
                                                                                       (1.47)

где 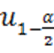 — квантиль нормального распределения порядка 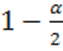, т.е. число , удовлетворяющее условию

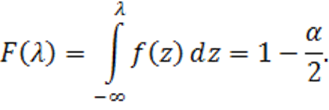
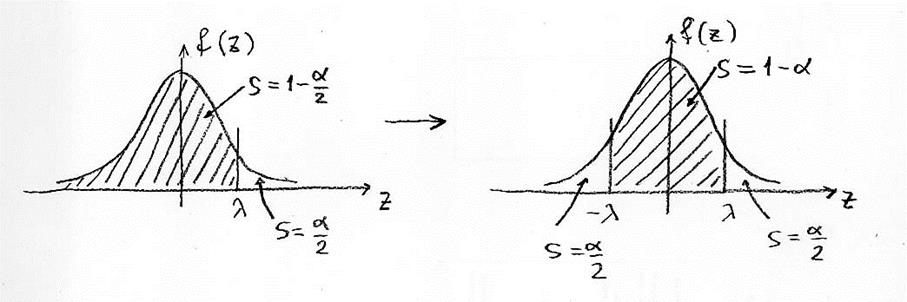
Следовательно, выполняется соотношение

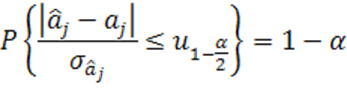
                                                                                       (1.48)

или иначе

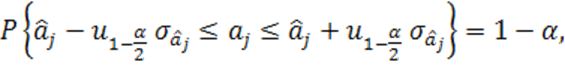
                                                                                       (1.49)

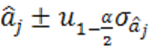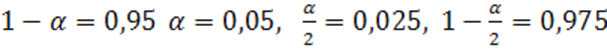а значит, найдены границы доверительного интервала , соответствующего доверительной вероятности . В частности, при  и по таблице значений  находим , т.е. если мы согласны на ошибку в 5% случаев, то можем руководствоваться «правилом ».