Векторная алгебра. Анализ функции одной переменной. Равенства векторов и разновидность векторов. Дифференцируемая функция. Вычисление расстояния от точки до прямой, страница 3

 

 

  .

  Чаще всего в качестве базиса выбирают взаимно перпендикулярные векторы единичной длинны.

  В трехмерном случае стандартное обозначение этих векторов: , , векторы попарно перпендикулярны. Такой базис называется декартовым.

Коллинеарность векторов.

  Векторы называются коллинеарными, если они связаны операцией умножения на константу: . Следовательно, координаты этих векторов должны быть связаны: , , .

  Если не оговорено другое, будут использоваться декартовы базисы.

Скалярное произведение векторов.

  Скалярное произведение сопоставляет паре векторов число. Используемое обозначение: .

  Скалярное произведение вычисляется по формулам:

1. 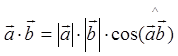 - бескоординатная формула

2.  - векторы заданы декартовыми координатами.

  Когда оба сомножителя одинаковы, скалярное произведение дает квадрат длинны вектора: .

  Скалярное произведение используется в геометрических задачах для записи условия перпендикулярности векторов. Для перпендикулярных (ортогональных) векторов скалярное произведение обращается в ноль.

  При помощи скалярного произведения можно вычислить угол между векторами, найдя его косинус.

Скалярное произведение и декартовы координаты.

  Скалярное произведение позволяет вычислить проекцию вектора на направление задаваемое другим вектором:

, 

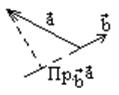
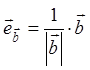
  В частности, и декартовы координаты любого вектора, можно представить через скалярное произведение: , ,

Главные свойства скалярного произведения.

1.  Симметрия при перестановке сомножеств.

2.  Линейность по каждому из сомножителей:

Векторное произведение.

  Векторное произведение двух векторов является вектором.

  Обозначение: .

Бескоординатная формула для векторного произведения.

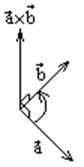Направление векторного произведения задается правилом правого винта (правой руки).

  Длинна векторного произведения вычисляется по формуле: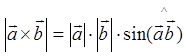

Основные свойства векторного произведения.

1.  Антисимметрия при перестановке сомножеств:

2.  Линейность по отдельным сомножителям:

  Примечания.

1.  Векторное произведение является стандартной операцией для построения вектора, который должен быть перпендикулярен заданной паре векторов.

2.  По длине векторного произведения находится площадь параллелограмма (треугольника) построенного на сомножителях.

Вычисление векторного произведения через декартовы координаты сомножителей.

  Когда сомножители заданы координатами, то векторное произведение вычисляется по формуле:

.

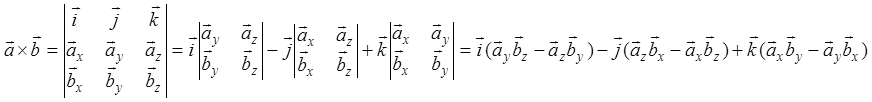Лекция №4. Дифференцируемая функция. (14.09.00)

  Функция называется дифференцируемой в точке a, если ее приращение в этой точке является линейной функцией Dx=x-a с точностью до бесконечно малых более высокого порядка: .

  Числовой множитель при  называется производная функции в точке a.

  Из этого определения сразу следует формула вычисления производной при помощи процедуры предельного перехода: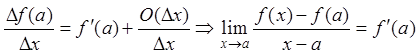

Правила дифференцирования.

  Множество значений переменной из области в которой производная существует называется областью существования функции .

  Дифференцирование – операция которая сопоставляет исходной функции ее производную всюду на : .

              Правила.

1. Производная линейной комбинации двух функций является линейной комбинацией производных: . Частный случай: постоянный множитель можно выносить за знак операции дифференцирования: .

  Из этого правила как частный случай следуют производные суммы и разности.

Идея доказательства.

  Берем точку a в которой производная существует и пишем в точке приращение функции: ,  и образуем линейную комбинацию выражений: , делим на Dx и переходим к пределу : .

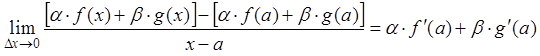2. Вычисление производной произведения.

Доказательство формулы.

, используя эти формулы, легко подсчитать приращение произведения этой функции: , делим на : .

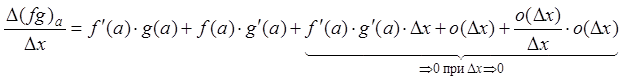3. Дифференцирование сложной функции. Сложные функции формируются при встраивании одной функции «внутрь» (в качестве аргумента) в другую функцию. Сложные функции также называются композициями функции.