Векторная алгебра. Анализ функции одной переменной. Равенства векторов и разновидность векторов. Дифференцируемая функция. Вычисление расстояния от точки до прямой, страница 2

  Пример: 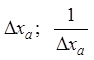.  является бесконечно большой при x®a и бесконечно малой при x®±¥.

Алгебра бесконечно больших и бесконечно малых.

Понятия о неопределённых выражениях:

  Сумма двух бесконечно малых является бесконечно малой.

  Умножение бесконечно малой на конечную является бесконечно малая.

  Умножение двух бесконечно малых является бесконечно малая.

  Сумма двух бесконечно больших одинакового знака есть бесконечно большая.

  Произведение двух бесконечно больших есть бесконечно большая.

  Во всех остальных случаях получаются неопределенные выражения – неопределенности. С каждой неопределенностью приходится работать отдельно.

Использование односторонних предельных переходов для описания свойств разрывных функций.

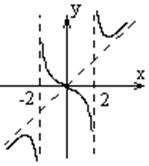
  При работе с разрывными функциями часто надо указывать с какой стороны множество приближается к точке разрыва, для этого вводятся специальные символы:

   или  - x приближается к a справа, т.е. x-a>0.

   или  - x приближается к a слева, т.е. x-a<0.

, и т.д.

Сравнение бесконечно малых и символы сравнения.

  Даны две бесконечно малых вблизи a функции:  и .

  Надо сравнить какая из них «меньше». Бесконечно малые сравниваются при помощи операции деления. Если 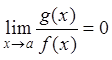, то говорят, g имеет более высокий порядок малости, по сравнению с f и пишут g(x)=o(f(x)). Если это так, то для суммы можно написать приближенную формулу: .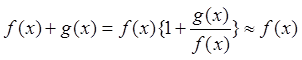

  Если 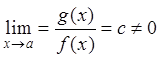, то говорят что бесконечно малые одного порядка.

Лекция №3. Равенства векторов и разновидность векторов. (11.09.00)

Разновидности векторов.

              Первая разновидность – связанные векторы.

  Связанный вектор – упорядоченная пара точек. Для него начало и конец зафиксированы. Каждый связанный вектор уникален – равных ему нет.

              Вторая разновидность – скользящие векторы.

  В случае скользящих векторов равными считаются векторы имеющие одинаковую длину, направление и начальные точки расположены на одной прямой.

  Скользящие векторы применяются в механике.

              Третья разновидность – свободные векторы.

  Здесь равными считаются любые векторы имеющие одинаковую длину и направление. Для свободных векторов положение начальной точки не имеет значения.

Линейные операции над векторами.

  Линейной комбинацией векторов a₁; a₂; a₃; …a_n с коэффициентами a₁; a₂; a₃; …a_n называется сумма .

  Сумма и разность являются частными случаями линейной комбинации.

  Главное свойство линейной комбинации векторов – неизменность при перестановке слагаемых.

  Вычисление линейной комбинации проводится по парному суммированию.

Понятие линейной независимости векторов.

  Векторы называются линейно-независимыми если их линейная комбинация обращается в ноль только тогда, когда все коэффициенты равны 0.

  Через максимальное число линейно-независимых векторов определяется размерность пространства.

  Размерность пространства – максимальное число линейно-независимых векторов в нем.

  Пример 1. Прямая.

.

  Любой вектор на прямой может быть получен растяжением некоторого известного вектора.

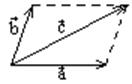
  Пример 2. Плоскость.

.

  На плоскости любая пара векторов не лежащая на одной прямой является линейно-независимой. Любой вектор на плоскости может быть представлен линейной комбинацией этой пары.

  Пример 3. Любые три вектора не расположенные в одной плоскости являются в трехмерном пространстве линейно-независимыми, т.е. любой вектор в пространстве представляется в виде: , где  - линейно независимые векторы.

Базис пространства.

  Любой максимальный набор линейно-независимых векторов образует в пространстве базис.

  Любой вектор в пространстве может быть записан как линейная комбинация векторов базиса. Числовые коэффициенты в этой линейной комбинации называются координатами вектора относительно выбранного базиса.

  Когда базис выбран, линейные операции над векторами можно свести с линейными операциями над координатами следующим образом:

 

 

 

  другая форма записи: