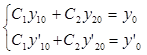 где
С1 и С2 неизвестные.
где
С1 и С2 неизвестные.
Все у известные числа, вычисленные при х=х0. Чтобы система имела решение при любых правых частях, необходимо и достаточно, чтобы основной определитель был отличен от 0.
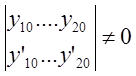 определитель
Вронского. Если определитель равен 0, то система имеет решение только при
условии, что есть пропорция начальных условий. Поэтому из этого следует, что
выбор начальных условий подчинен закону, так что любые начальные условия взять
нельзя, а это есть нарушение условия задачи Коши.
определитель
Вронского. Если определитель равен 0, то система имеет решение только при
условии, что есть пропорция начальных условий. Поэтому из этого следует, что
выбор начальных условий подчинен закону, так что любые начальные условия взять
нельзя, а это есть нарушение условия задачи Коши.
Если 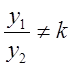 ,
то определитель Вронского не равен 0, ни при каких значениях х0.
,
то определитель Вронского не равен 0, ни при каких значениях х0.
Доказательство. Пусть
определитель равен 0, но 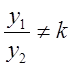 , выберем
начальные ненулевые условия y=0, y’=0. Тогда получим следующую систему:
, выберем
начальные ненулевые условия y=0, y’=0. Тогда получим следующую систему:
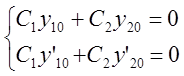
Эта система имеет бесконечное множество решений, когда определитель равен 0. С11 и С12 – решения системы.
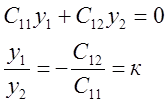
Это противоречит первому
случаю, а значит определитель Вронского не равен 0, при любых х0,
если 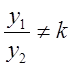 . Всегда из общего решения можно
выделить частное решение при
. Всегда из общего решения можно
выделить частное решение при 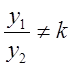 .
.
Билет №33
Теорема о структуре общего решения линейного однородного дифференциального уравнения 2-ого порядка с доказательством.
Теорема об общем решении дифференциального уравнения:
![]()
![]() решения
этого уравнения, то и функция
решения
этого уравнения, то и функция ![]() тоже решение. На
основе этой теоремы можно сделать вывод о структуре общего решения однородного
уравнения: если у1 и у2 есть решения дифференциального
уравнения, такие что их отношения не равны константе, то линейная комбинация
этих функций является общим решением дифференциального уравнения. Тривиальное
решение (или нулевое) не может служить решением этого уравнения.
тоже решение. На
основе этой теоремы можно сделать вывод о структуре общего решения однородного
уравнения: если у1 и у2 есть решения дифференциального
уравнения, такие что их отношения не равны константе, то линейная комбинация
этих функций является общим решением дифференциального уравнения. Тривиальное
решение (или нулевое) не может служить решением этого уравнения.
Доказательство:
![]() .
.
Билет №34
Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-ого порядка с доказательством.
Пусть дано уравнение с правой
частью: ![]() . Уравнение без правой части
. Уравнение без правой части
![]() если
вместо функции поставить 0 назовем характеристическим.
если
вместо функции поставить 0 назовем характеристическим.
Теорема о структуре общего решения уравнения с правой частью.
Т.1 Общее решение уравнения справой частью можно составить как сумму общего решения уравнения без правой части и какого-нибудь частного решения данного уравнения.
Доказательство.
Обозначим через общее решение ![]() , а
, а ![]() какое-нибудь
частное решение данного уравнения. Возьмем функцию
какое-нибудь
частное решение данного уравнения. Возьмем функцию ![]() .
Имеем
.
Имеем
![]() ,
, ![]() .
.
Подставляя выражения для y, y’, y’’ в
левую часть уравнения найдем:Выражение в ![]() первой
квадратной скобке равно 0. А выражение во второй скобке равно функции f(x).
Следовательно, функция
первой
квадратной скобке равно 0. А выражение во второй скобке равно функции f(x).
Следовательно, функция ![]() есть решение
данного уравнения.
есть решение
данного уравнения.
Билет №35
Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами, Ф.С.Р. и общее решение в случае различных действительных корней, характеристические уравнения с доказательством.
Возьмем однородное линейное уравнение второго порядка с постоянными коэффициентами:
![]() ,
,
где а – это числа.
Попробуем удовлетворить
уравнению функцией вида ![]() . Отсюда имеем:
. Отсюда имеем:
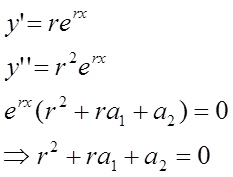
Отсюда видно, что ![]() будет решением данного уравнения,
если r будет корнем квадратного уравнения. Это уравнение
называется характеристическим. Чтобы составить характеристическое уравнение, надо
заменить у единицей, а каждую производную на r в степени
порядка производной.
будет решением данного уравнения,
если r будет корнем квадратного уравнения. Это уравнение
называется характеристическим. Чтобы составить характеристическое уравнение, надо
заменить у единицей, а каждую производную на r в степени
порядка производной.
1) Корни характеристического уравнения действительные и различные.
При этом оба корня могут быть
взяты в качестве показателей r функции ![]() . Здесь сразу можно
получить два уравнения. Ясно что их отношение не равно постоянной величине.
. Здесь сразу можно
получить два уравнения. Ясно что их отношение не равно постоянной величине.
Общее решение в случае действительных и разных корней дается формулой:
![]() .
.
Билет №36
Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами, Ф.С.Р. и общее решение в случае кратных корней, характеристические уравнения с доказательством.
Корни действительного уравнения действительные и равные.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.