Билет №1.
В дифференциальном исчислении по заданной функции приходилось отыскивать производную. Теперь рассмотрим обратную задачу. По заданной функции f(x) восстановить такую функцию F(x) производная от которой равна этой функции.
f(x)=F’(x)
Такую функцию (F(x)) принято называть первообразной.
О.1 Первообразной для функции у=f(x) на замкнутом интервале a,b называется функция у=F(x) удовлетворяющая условию:
f(x)=F’(x) для
всех ![]() интервалу a,b.
интервалу a,b.
Вывод: если функция F(x) является первообразной для функции y=f(x), то и функция y=F(x) + C также первообразная для функции f(x).
Теорема о разности 2-х первообразных.
Т.1 Две первообразные данной функции могут отличаться только на слагаемую константу.
Дано: F1’(x)=f(x), F2’(x)=f(x), Док-ть: F1(x)-F2(x)=C.
Док-во: Обозначим функцию y= F1(x)-F2(x), y'= (F1(x)-F2(x))’= F’1(x)-F’2(x) – по определению f(x)-f(x)=0 => это может быть только в том случае когда у=С.
О.2 Совокупность всех первообразных для функции y=f(x) называется неопределенным интегралом.
![]()
Свойства неопределенного интеграла.
1) линейность
а) интеграл от суммы функций равен сумме интегралов этих функций.
![]()
Слева
имеем совокупность первообразных для функций f(x) и ![]() . Справа имеем ту же самую
совокупность. Док-ть: эти совокупности равны.
. Справа имеем ту же самую
совокупность. Док-ть: эти совокупности равны.
![]() ч.т.д.
ч.т.д.
б) постоянный множитель выносится за знак неопределенного интеграла.
![]() к – константа.
к – константа.
2) инвариантность формул интегрирования.
![]()
![]()
Формулы интегрирования не зависят от того является ли аргумент независимой переменной или функцией другого аргумента.
Билет №2.
Рассмотрим область плоскости XOY ограниченную отрезком a, b оси X, сверху графиком функции y=f(x), (f(x)>0) и прямыми x=a, a=b.

Найти
площадь. Для этого разобьем отрезок a, b точками ![]() на участки
на участки ![]() на
n частей. Криволинейная трапеция разобьется на узкие криволинейные
трапеции. Подсчитаем значения функции в точке Х4. Будем считать эту
узкую криволинейную трапецию за прямоугольник с основанием
на
n частей. Криволинейная трапеция разобьется на узкие криволинейные
трапеции. Подсчитаем значения функции в точке Х4. Будем считать эту
узкую криволинейную трапецию за прямоугольник с основанием ![]() и Рi. Тогда
площадь будет равна f(Pi)
и Рi. Тогда
площадь будет равна f(Pi)![]() . Площадь будет
состоять из суммы этих прямоугольников.
. Площадь будет
состоять из суммы этих прямоугольников.
![]() - интегральная сумма.
- интегральная сумма.
![]()
![]()
О.2 Таким образом если f(x)>0, то площадь криволинейной трапеции есть определенный интеграл по отрезку a, b от этой функции.
Билет №4
Основные свойства определенного интеграла по отрезку.
1) Линейность
а) ![]()
Доказательство: ![]()
б) 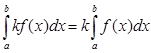 (док-во
аналогично с предыдущим)
(док-во
аналогично с предыдущим)
2) Аддитивности по отрезку
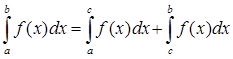
3) Интеграл от функции тождественно равной 1, равен длине этого отрезка
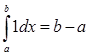
4) 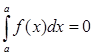 (вытекает
из геометрического смысла)
(вытекает
из геометрического смысла)
5) 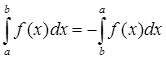 (вытекает
из геометрического смысла)
(вытекает
из геометрического смысла)
![]()
Билет №5
Теорема об оценке.
Т.1 Пусть значение функции в
точке р отрезка a, b удовлетворяет неравенству ![]() ,
тогда интеграл по отрезку a, b от этой функции удовлетворяет неравенству:
,
тогда интеграл по отрезку a, b от этой функции удовлетворяет неравенству:
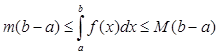
Доказательство:
(по опр.) ![]()
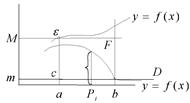
Геометрический смысл.
![]()
Криволинейная трапеция заключена между площадями прямоугольников с основаниями Р-а и высотами M и m.
Билет №6
«Теорема о среднем»
Т.1 Пусть есть точки ![]() тогда
тогда ![]()
![]() Эта
величина зависит от выбора точки и от числа n, но если n будет
увеличиваться, то различия между этими функциями будут исчезать. Среднее
значение функции на отрезке a, b будет равно пределу:
Эта
величина зависит от выбора точки и от числа n, но если n будет
увеличиваться, то различия между этими функциями будут исчезать. Среднее
значение функции на отрезке a, b будет равно пределу:
![]()
Формулировка:
Если функция ![]() непрерывна на замкнутом интервале a, b то
найдется точка
непрерывна на замкнутом интервале a, b то
найдется точка ![]() на этом отрезке, в которой
значение функции равно
на этом отрезке, в которой
значение функции равно ![]() , т.е.
, т.е. ![]() .
.
Доказательство:
По свойству функций непрерывных на замкнутом интервале, она достигает своего наибольшего и наименьшего значения, значит мы имеем условие «теоремы об оценке»:
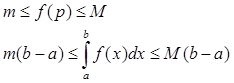
Разделим обе части на ![]()
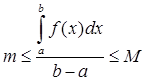
т.к. 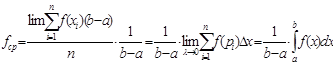
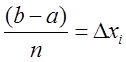 и
получаем
и
получаем ![]()
По свойству непрерывных
функций на заданном интервале, функция приняв два значения в точках ![]() и
и ![]() обязательно
примет и противоположное значение между ними, которое равно
обязательно
примет и противоположное значение между ними, которое равно ![]() в некоторой точке
в некоторой точке ![]() .
.
Геометрический смысл:
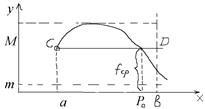
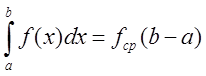
![]() (площади
треугольника с основанием
(площади
треугольника с основанием ![]() и высотой
и высотой ![]() ).
).
Билет №7
«Теорема Барроу» (теорема о производной интеграла с переменным верхним пределом).
Пусть на [a, b]
задана f(x). Рассмотрим 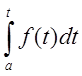
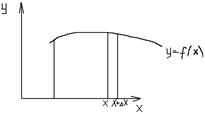
Геометрически заданный интервал представляет собой криволинейную трапецию с переменным основанием. Производная интеграла с переменным верхним пределом равна интегралу в точке верхнего предела.
Доказательство:
Обозначим 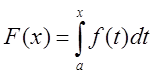 . Дадим точке х, приращение
. Дадим точке х, приращение ![]() . Тогда функция
. Тогда функция ![]() получит приращение
получит приращение ![]() .
.
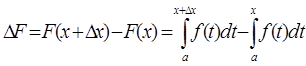
по определению производной 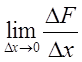 - задача
- задача
(по свойству аддитивности):
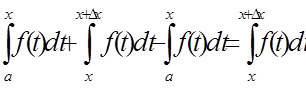
т.е. 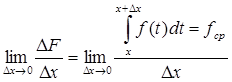
по «теореме о среднем» есть ![]() в которой значение функции будет
равно
в которой значение функции будет
равно ![]()
![]() .
.
Билет №23
О.1 Дифференциальным уравнением называется уравнение связывающее независимую переменную х и неполную функцию у и производную искомой функции y’.
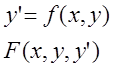 дифференциальное
уравнение 1-го порядка.
дифференциальное
уравнение 1-го порядка.
![]()
Если сложная функция у есть функция одной переменной, то дифференциальное уравнение называется обыкновенным.
О.2 Порядком дифференциального уравнения называется порядок степени производных, входящих в уравнение.
О.3 Решением (интегрированием) дифференциального уравнения называется интеграл от функции которая будучи подставленной в уравнение превращает его в тождество.
Виды дифференциальных уравнений 1-го порядка:
1. С разделяющимися переменными
2. Однородное
3. Линейное
4. Уравнение Бернулли.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.