Рентгенографическое исследование фибриллярных структур. Рентгендифракционные исследования мышц (Разделы 3-4 учебного пособия "Рентгенография биологических объектов")

3. Рентгенографическое исследование

фибриллярных структур

Кроме глобулярных белков, метод изучения структуры которых был рассмотрен в предыдущем параграфе, существуют также фибриллярные структуры, к которым относятся некоторые фибриллярные белки (например, коллаген, кератин, мышечные белки), а также ДНК. Характерной для фибриллярных структур является периодичность вдоль одного направления, что дает возможность исследовать их рентгенографически. По сравнению с кристаллами белков такие структуры менее упорядочены. Поэтому не удается получить таких же детальных сведений о структуре, которые возможны при исследовании кристаллов. Тем не менее путем построения моделей пространственной структуры, которые хорошо согласуются с рентгенографическими и другими данными, метод позволяет получить очень важную информацию о фибриллярных структурах.

Простейшим примером фибриллярной структуры является одномерная точечная решетка, то есть ряд точек, отстоящих друг от друга на расстояние С (рис. 3.1). Направления, в которых происходит усиление рассеянного излучения при нормальном падении первичного пучка, определяется соотношением

                                   ,                                                     (3.1)

где  – целые числа. Если же первичный пучок падает под некоторым углом  к направлению ряда, то выражение, аналогичное формуле (3.1), будет

                               .                                          (3.2)

Если периодичность фибриллярной структуры определяется вектором , то структурная амплитуда имеет вид

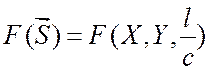                                                                               (3.3)

и отлична от нуля на плоскостях обратного пространства при 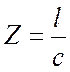. Эти плоскости, называемые «слоевыми», находятся на расстоянии 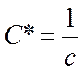  друг от друга. Так как в направлениях  и  периодичность отсутствует, то амплитуда (3.3) вдоль слоевых плоскостей является непрерывной функцией и, подобно (2.10), для нее может быть записано выражение

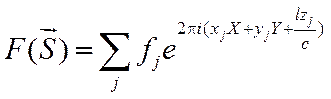                             .                               (3.4)

Рис. 3.1. Схема образования дифракционной картины

от одномерной решетки

Если воспользоваться понятием сферы Эвальда, то можно видеть, что в обратном пространстве слоевые плоскости, пересекая эту сферу, дают сечения сферы, приводящие к образованию на рентгенограмме слоевых линий. Поэтому характерным признаком дифракционных картин от фибриллярных структур является наличие на них слоевых линий (рис. 3.2). Можно отметить, что наличие слоевых линий на рентгенограммах имеет место в случае дифракции как от одиночных, например цепочечных, молекул, так и от их агрегатов, характеризующихся параллельным расположением таких молекул. Примером подобной структуры является осевая текстура, в которой оси молекул в достаточной степени параллельны одному выделенному направлению, тогда как другие оси имеют произвольную ориентацию. Поэтому осевая текстура имеет одну ось симметрии бесконечного порядка.

Рис. 3.2. Схема возникновения слоевых линий

на рентгенограмме от фибриллярной структуры

Фибриллярные структуры, будучи упорядоченными в одном направлении, являются частным случаем кристаллов, имеющих периодичность в трех измерениях. Исходя из этого установление распределения электронной плотности таких структур по распределению интенсивностей на рентгенограмме осуществляют, как и в случае кристаллов, с помощью синтеза Фурье.

Для систем с одномерной упорядоченностью в большинстве случаев используют цилиндрические, а не декартовы координаты. Особенно такие координаты удобны, если биологический образец обладает круговой симметрией, то есть в нем присутствуют простая или винтовая оси симметрии.

Положение точек в пространстве в цилиндрических координатах задается радиусом , полярным углом  и высотой . Тогда связь между декартовыми и цилиндрическими координатами в реальном и обратном пространствах имеет соответственно вид

                              ;                             (3.5)

                             .                        (3.6)

Схематически соотношение между декартовыми и цилиндрическими координатами представлено на рис. 3.3. После подстановки выражений (3.5) и (3.6) в (1.9) и (2.13) получают прямое и обратное преобразования Фурье в цилиндрических координатах

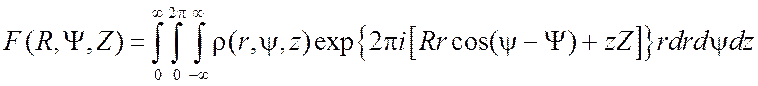, (3.7)

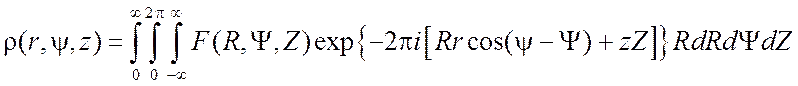.(3.8)

Рис. 3.3. Декартовы и цилиндрические координаты

в реальном (а) и обратном (б) пространствах

Уравнения (3.7) и (3.8) являются наиболее общими. Для частного случая, например цепной молекулы, из общей зависимости  можно выделить зависимость  от  и  (или  от  и ). В этом случае задача сводится к двумерной задаче в координатах  и .

Если положить  и отвлечься от зависимости от  и , то из теории следует, что интегралы Фурье (3.7) и (3.8) можно выразить через функции Бесселя

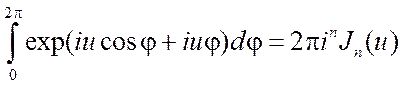                      ,                             (3.9)

где  – бесселевы функции -го порядка ( – целое число), а . Поэтому функции Бесселя играют существенную роль при решении задач в цилиндрических координатах. Из рис. 3.4 видно, что первый максимум функций Бесселя с увеличением n сдвигается от начала координат и только функция  отлична от нуля в начале координат. У всех функций наблюдается чередование максимумов и минимумов, так что величина экстремумов постепенно уменьшается при увеличении расстояния от начала координат и числа .

Рис. 3.4. Зависимость функций Бесселя от расстояния

от начала координат u и порядкового номера n

В наиболее простом случае цилиндрической симметрии, когда , соотношение (3.7), если опустить координаты  и  и принять во внимание (3.9) для , дает

                                .                            (3.10)

Аналогично из формулы (3.8) получаем обратное к (3.10) соотношение

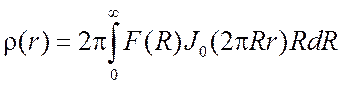                              .                            (3.11)

Поэтому аналогично интегралу Фурье имеет место также интеграл Фурье-Бесселя, обладающий свойством обратимости.

Нахождение трансформанты Фурье в общем случае более сложно, и можно показать, что оно в конечном счете сводится к следующему. Сначала раскладывают  в ряд Фурье по  и находят коэффициенты

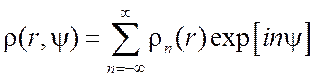                                ,                              (3.12)

где

                              .                      (3.13)

Затем определяют трансформанты Фурье-Бесселя

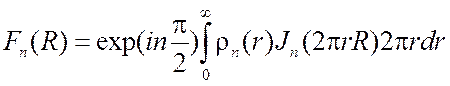                                           (3.14)

и суммируют ряд Фурье по

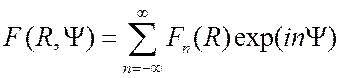                               .                           (3.15)

Если объединить две последние формулы, то окончательно получим

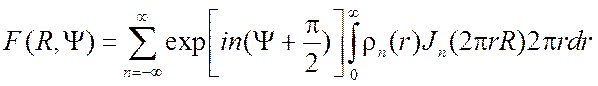            ,         (3.16)

где  дается выражением (3.13).

Аналогичным образом можно получить обратную трансформанту Фурье-Бесселя

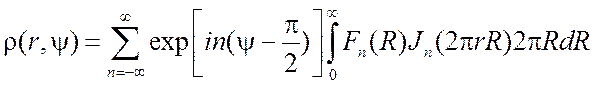         ,             (3.17) где  определяется по формуле .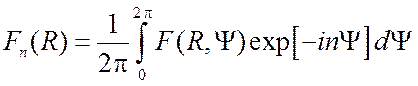

На основе полученных формул решены наиболее важные модельные задачи, такие как рассеяние сплошным цилиндром заданного радиуса, рассеяние полыми цилиндрами со стенками конечной и бесконечно малой толщины, рассеяние столбчатыми структурами, то есть структурами, электронная плотность которых изменяется в зависимости от  по закону

.

Трансформанта Фурье  столбчатых структур существует только при , давая нулевую слоевую линию.