1.
а) 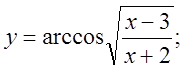 б)
б) 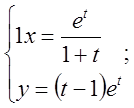 в)
в)
![]() г)
г) ![]()
2.
а) 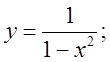 б)
б) 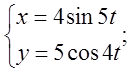 в)
в) ![]()
3.
![]() 4.
4. 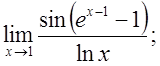 5.
5. 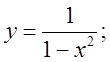
6. ![]() 7.
7. 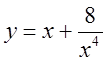
![]() 8.
8. 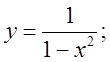
Варіант 21.
1. а) 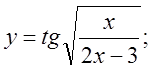 б)
б) 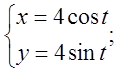 в)
в) ![]()
г) ![]()
2. а) 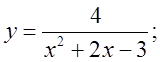 б)
б) 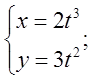 в)
в) 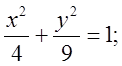
3. ![]() 4.
4. 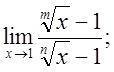 5.
5. 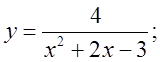
6. 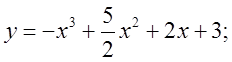 7.
7. ![]()
![]() 8.
8. 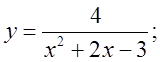
Варіант 22.
1.
а) ![]() б)
б) 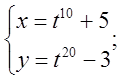 в)
в) ![]()
г) ![]()
2.
а) 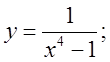 б)
б) 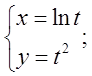 в)
в) ![]()
3.
![]() 4.
4. 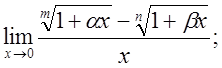 5.
5. 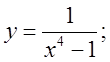
6. ![]() 7.
7. ![]()
![]() 8.
8. 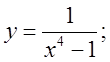
Варіант 23.
1. а) ![]() б)
б) 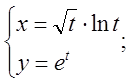 в)
в) ![]()
г) ![]()
2. а) 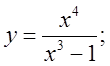 б)
б) 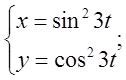 в)
в) ![]()
3. ![]() 4.
4. 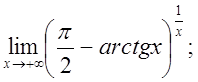 5.
5. 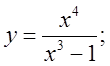
6. ![]() 7.
7. 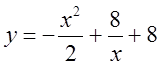
![]() 8.
8. 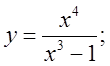
Варіант 24.
1.
а) ![]() б)
б) 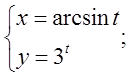 в)
в) ![]()
г) ![]()
2.
а) 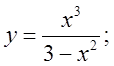 б)
б) 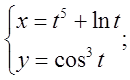 в)
в) ![]()
3.
![]() 4.
4. ![]() 5.
5. 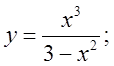
6. 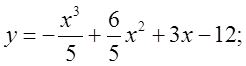 7.
7. ![]()
![]() 8.
8. 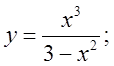
Варіант 25.
1.
а) 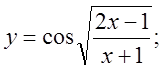 б)
б)
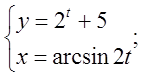 в)
в) ![]()
г) ![]()
2.
а) 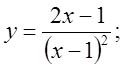 б)
б) 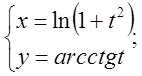 в)
в) ![]()
3.
![]() 4.
4. 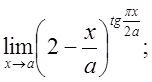 5.
5. 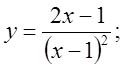
6. ![]() 7.
7. 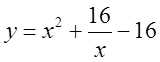
![]() 8.
8. 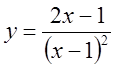
Додаткове завдання.
1. Пружна лінія бруса, один бік якого закріплений до стінки, а другий лежить на підпорі, має рівняння
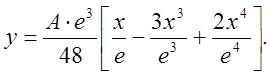
Знайти найбільший прогин бруса.
2. Брус вимилюється з косового ситовна діаметром d. Міцність прямокутного бруса пропорційна до його товщина та квадрата висоти. Підібрати розміри бруса так, щоб міцність була найбільшою.
3. Вікно має форму прямокутника, замкненого півколом. Обчислити розміри цього вікна даного периметра, щоб площа його була найбільша.
4. Міщність прямокутного бруса пропорційна до його товщини та куба висоти. Обчислити товщину бруса найбільшої міцності, який можна вирізати з колоди діаметром 16 см.
5. Знайти найекономніші розміри циліндричного парового казана об’єму v.
6. На якої висоті ![]() перпендикуляра до стола
треба повісити електричну лампу, щоб найкраще освітити точку
перпендикуляра до стола
треба повісити електричну лампу, щоб найкраще освітити точку ![]() на столі? (див. рис. 8).
на столі? (див. рис. 8).
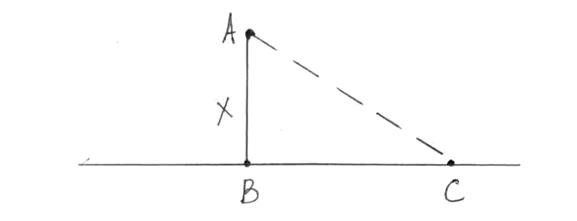 |
Рисунок 8
7. З половини колоди, діаметр якої 40 см, треба вирізати прямокутний брус. Обчислити сторони прямокутного перерізу бруса, щоб опір на стиск був максимальним.
8. Обчислити розміри конічного шатра даної місткості, який потребує найменше матерії.
9. Знайти похідні алгебраїчної суми складених функцій, виконувавши тотожні перетворення:
Приклади.
1. ![]()
2. 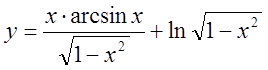
3. 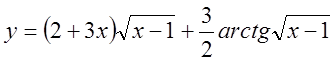
4. 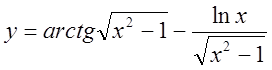
5. 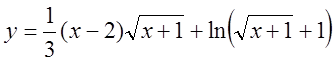
6. 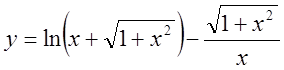
Глава III. Елементи лінійної та
векторної алгебри
3.1 Визначники та їх властивості
Означення 1. Матрицею розміру ![]() називають прямокутну
таблицю з m рядків і n
стовпців, складену з
називають прямокутну
таблицю з m рядків і n
стовпців, складену з ![]() елементів (чисел, або
інших об’єктів).
елементів (чисел, або
інших об’єктів).
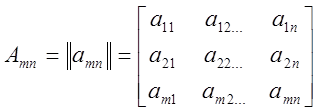 (1)
(1)
де ![]() - елементи матриці,
- елементи матриці,
![]() - рядки
- рядки![]()
![]() - стовпці.
- стовпці.
Означення 2. Якщо ![]() , то матрицю називають
квадратною.
, то матрицю називають
квадратною.
Кожній квадратній матриці відповідає визначник
![]()
Означення 3. Визначником ![]() того порядку називається
число, або числова функція, яка позначається
того порядку називається
число, або числова функція, яка позначається
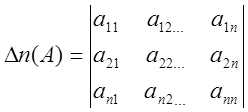 (2)
(2)
і обчислюється за певним правилом.
Визначники бувають 1-го – порядку – це
звичайне число ![]() 2-го - порядку
2-го - порядку
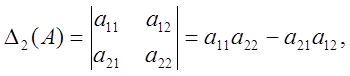
тобто при ![]()
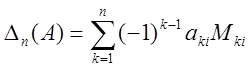 (3)
(3)
де ![]() ,
, ![]() -
елементи і-того стовпця, а
-
елементи і-того стовпця, а ![]() - визначник матриці
порядку (n-1), одержаної з Аnn вилученням її
к-того рядка та і-того стовпця.
- визначник матриці
порядку (n-1), одержаної з Аnn вилученням її
к-того рядка та і-того стовпця.
Цей визначник ![]() називається
мінором порядка
називається
мінором порядка ![]() матриці
матриці ![]()
Зауваження. Тільки знаючи формулу для визначника матриці порядку ![]() можна одержати формулу для визначника
матриці порядку n.
можна одержати формулу для визначника
матриці порядку n.
Тепер розглянемо властивості визначників, які використовуються для спрощення обчислення визначників великого порядку.
1. Визначник не зміниться, якщо рядки його замінити стовпцями і навпаки, тобто
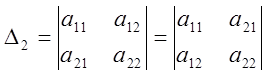
Ця властивість називається властивістю транспонування, вона перевіряється безпосереднім обчисленням.
2. Якщо матриця ![]() має нульовий ряд, то
визначник
має нульовий ряд, то
визначник
![]()
3. Якщо матриця ![]() має два рівних ряди, то
визначних
має два рівних ряди, то
визначних
![]()
4. Загальний множник будь-якого ряду можна винести за знак визначника.
5. Якщо елементи двох паралельних рядів відповідно рівні, або пропорційні, то такий визначник дорівнює 0.
6. При перестановці двох паралельних рядів місцями визначник змінює знак на протилежний, тобто
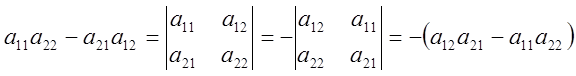
7. Якщо матриця ![]() одержана з матриці
одержана з матриці ![]() додаванням до і-того ряду, її
паралельного j-того ряду
помноженого на довільне число к, то
додаванням до і-того ряду, її
паралельного j-того ряду
помноженого на довільне число к, то ![]() Це
доводиться перевіркою, тобто
Це
доводиться перевіркою, тобто
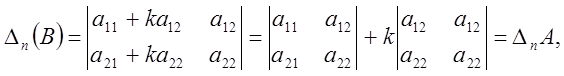
тому що 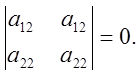
3.2 Системи лінійних алгебраїчних рівнянь (СЛАР)
Формули Крамера
Розглянемо систему m лінійних рівнянь з n невідомими, тобто:
![]() (1)
(1)
де ![]() - задана матриця, або основна
матриця системи. Матриця
- задана матриця, або основна
матриця системи. Матриця ![]() називається
розширеною матрицею системи (1).
називається
розширеною матрицею системи (1).
Нехай ![]() ,
тоді
,
тоді
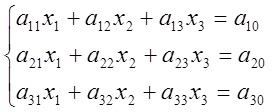 (2)
(2)
Якщо стовпець вільних членів 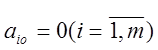 , то система називається однорідною.
, то система називається однорідною.
Означення 1. Розв’язком ЛСР(1) називають довільну трійку чисел (![]() ), яка задовольняє кожному з рівнянь
системи.
), яка задовольняє кожному з рівнянь
системи.
Система може мати єдиний розв’язок (система визначена), безліч розв’язків (система сумісна, але невизначена), зовсім їх не мати (система несумісна).
Теорема Крамера. (сумісність і визначеність системи).
1. Якщо головний визначник системи ![]() ,
то система (2) має єдиний розв’язок, який знаходиться за формулами
,
то система (2) має єдиний розв’язок, який знаходиться за формулами
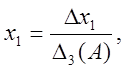
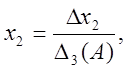
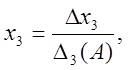 (3), де
(3), де
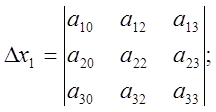
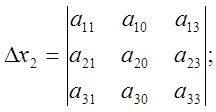
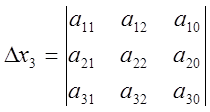
2. Якщо ![]() і хоча б один з побічних
визначників
і хоча б один з побічних
визначників ![]() ,
, ![]() ,
,
![]() відмінний від нульові, то система (2)
не має аніякого розв’язку (система (2) несумісна).
відмінний від нульові, то система (2)
не має аніякого розв’язку (система (2) несумісна).
3. Якщо ![]() і відповідна її однорідна
система має більше, ніж один розв’язок, то система (2) має безліч
розв’язків, тобто вона сумісна і невизначена. Зауважимо, що формули Крамера (3)
застосовують, як правило, для
і відповідна її однорідна
система має більше, ніж один розв’язок, то система (2) має безліч
розв’язків, тобто вона сумісна і невизначена. Зауважимо, що формули Крамера (3)
застосовують, як правило, для ![]() .
.
Приклад. Розв’язати за формулами Крамера систему:
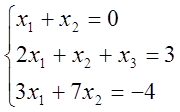
Розв’язання.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.