Зауваження. Розглянуті властивості дають можливість перетворити векторну суму ![]() за тими самими правилами, що й
звичайну алгебраїчну суму, а саме: зводити подібні члени, розкривати дужки
тощо.
за тими самими правилами, що й
звичайну алгебраїчну суму, а саме: зводити подібні члени, розкривати дужки
тощо.
Означення 6. Вектор ![]() називається лінійною
комбінацією векторів
називається лінійною
комбінацією векторів ![]() , якщо існують одночасно
ненульові
, якщо існують одночасно
ненульові ![]() , такі, що
, такі, що ![]()
Два колінеарних вектори завжди
знаходяться в лінійній залежності, а векторна рівність (1) ![]() є умовою колінеарності.
є умовою колінеарності.
Означення 7. Вектори називаються компланарними, якщо вони знаходяться в одній
площині або в паралельних площинах. При компланарних вектори завжди знаходяться
в лінійній залежності, а векторна рівність (2) ![]() є
умовою компланарності.
є
умовою компланарності.
Чотири й більше вектори завжди лінійно залежні і розкладання
![]() (3)
(3)
можна здійснити лише єдиним способом.
Означення 8. Сукупність лінійно незалежних векторів, за якою можна розкласти
довільний вектор, називається базисом. Звідси випливає, що на площині базисом
можуть бути довільні два не колінеарні вектори, а в просторі ![]() - довільні три некомпланарних вектори.
- довільні три некомпланарних вектори.
Співвідношення (2) називають
розкладом вектора ![]() за базисом
за базисом ![]() і
і ![]() ,
аналогічно в
,
аналогічно в ![]() співвідношення (3)
називається розкладом будь-якого вектора
співвідношення (3)
називається розкладом будь-якого вектора ![]() за
базисом
за
базисом ![]() .
.
При цьому скаляри ![]() називають координатами, а вектори
називають координатами, а вектори ![]() - компонентами, або складовими
вектора
- компонентами, або складовими
вектора ![]() за базисом
за базисом ![]() .
.
3.6 Проекція вектора на вісь.
Декартів прямокутний координатний базис
Означення 1. Координатною прямою (віссю) називається пряма, на якої вибрано напрям, фіксована точка О – початок координат, а також масштаб – відрізок, довжина якого приймається за одиницю. Причому з правого боку від точки О точкам прямої ставляться у відповідність додатні числа, а з іншого боку – точкам прямої відповідають від’ємні числа.
Теорема. Кожному дійсному числу х із нескінченної множини R можна поставити у відповідність точку на координатній прямій і така відповідність є взаємно однозначною.
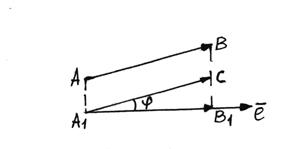
Означення 2. Проекцією вектора ![]() на вісь
на вісь ![]() називають число, а саме:
називають число, а саме:
|
||||
 |
||||
|
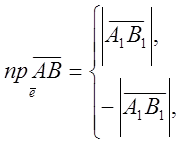
|
Існує теорема. Проекція вектора на вісь дорівнює додатку модуля вектора на косинус кута між вектором і віссю, тобто
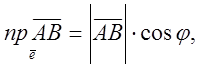 (1)
(1)
де ![]() - кут між
- кут між ![]() і
віссю
і
віссю ![]() (мал. 10), оскільки
(мал. 10), оскільки ![]() - паралелограм.
- паралелограм.
Тобто, якщо 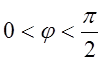 -
гострий, число додатне
-
гострий, число додатне
якщо
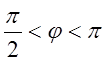 - тупий, число від’ємне.
- тупий, число від’ємне.
Очевидно, що коли ![]() , то
, то 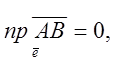 і
навпаки.
і
навпаки.
Властивості проекції вектора на вісь.
1. Скалярний множник можна виносити за знак проекції, тобто
![]() (2)
(2)
2. Проекція суми векторів на вісь дорівнює сумі проекції складових векторів на ту саму вісь, тобто
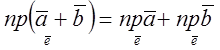 (3)
(3)
Властивість 2 узагальнюється на випадок довільного скінченного числа векторів.
Означення 3. Три взаємно перпендикулярні координатні прямі, які мають спільний
початок координат і єдиний масштаб утворюють декартову систему координат у
просторі. Напрям осей ![]() можна задати одиничними
векторами
можна задати одиничними
векторами ![]() , тобто
, тобто ![]() ,
,
![]()
![]()
![]()
Означення 4. Трійка ортів ![]() називається також координатним
декартовим базисом.
називається також координатним
декартовим базисом.
Таким чином, для кожної точки Р
простору можна поставити у відповідність впорядковану трійку чисел ![]() , які є координатами точки
, які є координатами точки ![]() або координатами радіус-вектора
або координатами радіус-вектора ![]() (4).
(4).
Як видно, координати точки Р і радіуса-вектора точки Р збігаються.
Аналогічно формулі (1)
довільний вектор ![]() в декартовій системі
координат можна записати у вигляді:
в декартовій системі
координат можна записати у вигляді:
![]() (5)
(5)
де ![]()
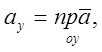
![]() - проекції вектора
- проекції вектора ![]() на осі координат називаються його
координатами
на осі координат називаються його
координатами ![]() .
.
Якщо вектор ![]() утворює
з осями координат кути
утворює
з осями координат кути ![]() , тоді згідно з (1)
маємо
, тоді згідно з (1)
маємо
![]()
![]()
![]() (6)
(6)
Звідки 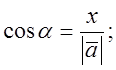
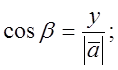
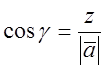 (7)
- напрямні косинуси вектора
(7)
- напрямні косинуси вектора ![]() , для яких
справджується рівність
, для яких
справджується рівність
![]() (8)
(8)
Координати вектора ![]() виражаються через координати його
початку
виражаються через координати його
початку ![]() та кінця
та кінця ![]() за
формулами
за
формулами
![]()
![]()
![]() (9)
(9)
Таким чином, довжина вектора ![]() , тобто відстань між точками А
і В, знаходиться за формулами
, тобто відстань між точками А
і В, знаходиться за формулами
![]() (10)
(10)
або
![]() (11)
(11)
Оскільки умова колінеарності векторів
рівносильна умові ![]() , тобто
, тобто ![]()
![]()
![]() , то звідти маємо
, то звідти маємо
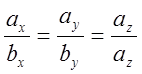
![]() (12)
(12)
Остання рівність виражає умову колінеарності векторів в координатній формі.
3.7 Скалярний добуток векторів та
його властивості
Означення. Скалярним добутком векторів ![]() і
і ![]() називається число (скаляр), яке
дорівнює добутку модулів цих векторів на косинус кута між ними, тобто
називається число (скаляр), яке
дорівнює добутку модулів цих векторів на косинус кута між ними, тобто
![]() (1)
(1)
Механічний зміст скалярного добутку
полягає в обчисленні роботи А під дією постійної сили ![]() при переміщені матеріальної точки
вздовж прямолінійного відрізка
при переміщені матеріальної точки
вздовж прямолінійного відрізка ![]() тобто
тобто
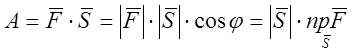
![]() (2)
(2)
Властивості скалярного добутку по означенню.
1).
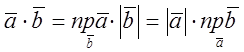
2).
![]() (комутативна або симетрична)
(комутативна або симетрична)
3).
![]() (позитивна),
(позитивна), ![]()
4).
![]() (білінійна або дистрибутивна)
(білінійна або дистрибутивна)
![]()
5) ![]() тобто умова перпендикулярності векторів,
наслідком якої є
тобто умова перпендикулярності векторів,
наслідком якої є ![]()
6) якщо ![]() є
орт вектора
є
орт вектора ![]() , то
, то 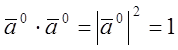 ,
або
,
або ![]()
7) ![]() (асоціативна).
(асоціативна).
Нехай задано два вектори в декартовій системі
координат ОХУZ: ![]() і
і ![]() .
Тоді за властивостями скалярного добутку отримаємо
.
Тоді за властивостями скалярного добутку отримаємо ![]() (3)
(3)
Тобто скалярний добуток двох векторів дорівнює сумі добутків однойменних координат цих векторів. Таким чином, можна записати в координатній формі всі одержані нами формули.
Наприклад, 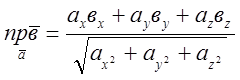 (4)
(4)
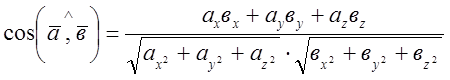 (5)
(5)
Умова перпендикулярності ![]() і
і ![]() , заданих координатами має вигляд
, заданих координатами має вигляд
![]() (6)
(6)
Приклад. Обчислити роботу сил ![]() [КГ] і
[КГ] і ![]() [КГ], якщо переміщення точки їх прикладання зображається
вектором
[КГ], якщо переміщення точки їх прикладання зображається
вектором ![]() [м].
[м].
Розв’язання.
![]() , де
, де ![]() ,
,
![]()
![]()
![]()
Відповідь: А = 11 [КГМ]
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.