Расчет серийного тягового электрического двигателя НБ – 514 и проверка оптимальности выбора параметров активного слоя его якоря, страница 2

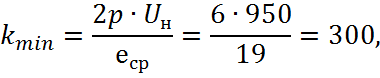
тогда

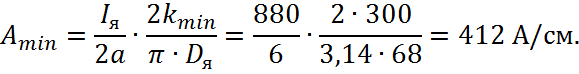
Минимальное коллекторное деление по технологическим соображениям (по условиям соединения коллекторной пластины с проводником обмотки) должно быть не менее 4÷4,5 мм.

Максимально допустимое по исполнению коллектора число коллекторных пластин:

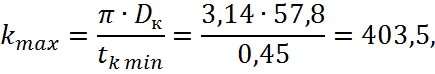
тогда

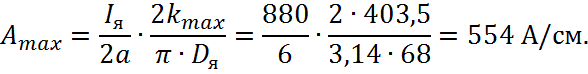
Наносим значения A_min и A_max на рис. 2 и выбираем из этого диапазона вариант с u_п = 8.

Границы допустимых значений A_min и A_max определяются минимальным и максимальным возможным числом коллекторных пластин k_min и k_max соответственно, т. е. ограничением межламельного напряжения.

Шаг 3. Расчет магнитной цепи ТЭД.

3.1.  Составим в масштабе 1:2 эскиз магнитной цепи (рис. 3). На эскизе показываем численные значения длин характерных участков магнитной цепи в сантиметрах.

3.2.  Эквивалентный воздушный зазор не рассчитываем, так как заданный ТЭД имеет компенсационную обмотку.

3.3.  Расчет коэффициента воздушного зазора, учитывающего повышение падения магнитного напряжения из-за зубчатой формы активного слоя ТЭД:

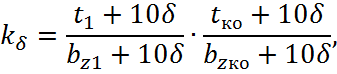
где t_ко – зубцовое деление компенсационной обмотки (принимаем по приложению 2, зная величину диаметра якоря определенной машины),

t_ко = 34,5 мм;

b_z1, b_{z ко} – ширина зубцов якоря и компенсационной обмотки по окружности якоря, b_{z ко} = 16 мм (приложение 2).

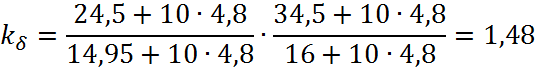
Расчетный зазор равен:

3.4.  Расчет падения магнитного напряжения в воздушном зазоре:

3.5.  Разбиваем магнитную цепь на участки:

а)   зубцовый слой якоря. По таблице 2.3 [1, стр. 599] определяем для  значение напряженности поля H_z = 515 А/см, длина магнитного пути в зубцах h_z0 = 4,169 см, тогда магнитная напряженность зубцов:

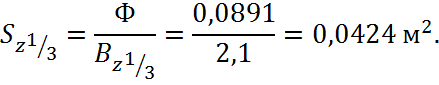
Результаты расчетов сводим в таблицу 2.

б)  сердечник якоря. При 2p = 6 принимаем B_я = 1,4 Т (стр. 133 [1], формула 2.207). По индукции B_я = 1,4 Т из таблицы 2.3 приложения 2 [1] находим напряженность H_я = 18,2 А/см.

Магнитный поток равен:

Длина магнитного пути в ярме якоря L_я = 13,4 см.

Магнитное напряжение в ярме якоря:

Определяем активную высоту сечения сердечника якоря:

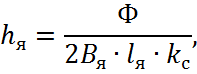
где  – коэффициент заполнения сердечника сталью.

 – для стали марки Э1300А.

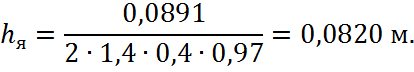
Сечение сердечника:

Число рядов каналов выбираем n_к = 2 (стр. 133 [1]) с диаметром d_к = 0,03 м (стр. 133 [1] формула 2.209).

Тогда, конструктивная высота сечения сердечника якоря равна:

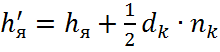 (стр. 133 [1] формула 2.210).

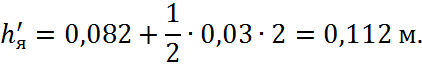
Внутренний диаметр сердечника якоря:

в)   зубцовый слой полюса (компенсационная обмотка).

Число витков компенсационной обмотки N_ко = 6, число пазов z_ко = 6, высота паза h_zко = 49 мм; геометрические размеры расположения пазов компенсационной обмотки:

C = 15 мм; В = 30 мм; А = 50 мм; b_пко = 19,5 мм; t_zко = 34,5 мм (приложение 2).

Площадь поперечного сечения зубцов полюса на расстоянии 1/3 от их головок, обращенных к якорю:

где  – число пазов на участке А;

0,97 – коэффициент заполнения сталью;

 – ширина паза, м;

 - длина сердечника (обычно равна длине сердечника якоря l_я), м.

где  - коэффициент рассеяния. Принимаем  ([1], формула 2.107).

Индукция:

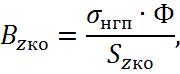
где Ф – рабочий магнитный поток полюса;

 – коэффициент рассеяния наконечника главного полюса.

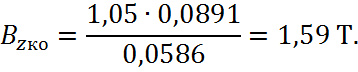
Для этой индукции по таблице 2.3 приложения 2 [1] напряженность:

Магнитное напряжение зубцового слоя компенсационной обмотки:

г)   сердечник полюса.

Индукцию в сердечнике принимаем равной:

 (стр. 135 [1], формула 2.217),

принимаем

Коэффициент рассеяния при 2p = 6 и наличии компенсационной обмотки σ = 1,25 (стр. 135 [1], формула 2.218).

Площадь сечения сердечника полюса:

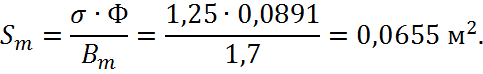
Ширина сердечника полюса:

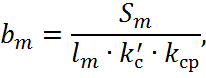
где  – коэффициент заполнения полюса сердечника сталью;

 – коэффициент, учитывающий подрезы сердечника полюса по углам для улучшения вписывания его во внутреннюю полость катушки;  так как медь катушки наматывается плашмя.

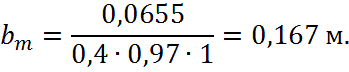
Полюсное деление:

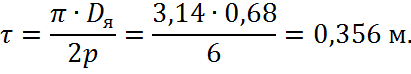
Высота сердечника полюса при 2p = 6:

 (стр. 136 [1])

Для индукции B_m = 1,7 Т по таблице 2.3 приложения 2 [1] напряженность сердечника главного полюса:

д)  стык полюс – ярмо:

е)   остов (ярмо).

Радиальная толщина остова:

где  – ширина сердечника главного полюса.

принимаем

Длина расчетного сечения:

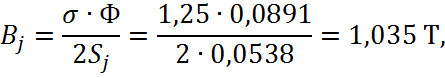
что удовлетворяет условию

Для этой индукции по таблице 2.3 приложения 2 [1] напряженность на участке между полюсами:

Диаметр внутренней поверхности круглого остова:

Внешний диаметр остова:

При 2p = 6 должно выполняться условие

 - условие выполнено.

Длина магнитного участка между полюсами

Магнитное напряжение участка между полюсами:

ж)   переход ярмо – полюс.

Магнитный поток:

Магнитная индукция в выходе (стр. 141 [1], формула 2.242):

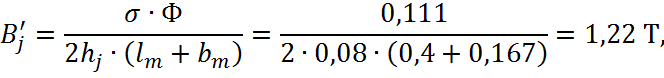
тогда

 (приложение 2, табл. 2.3 [1]).

Длина магнитного пути:

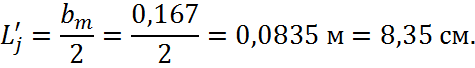
Площадь поперечного сечения:

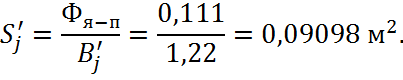
Магнитная напряженность участка:

з)   воздушный зазор.

Магнитный поток в воздушном зазоре:

Индукция в воздушном зазоре:

Магнитная напряженность участка:

Длина расчетного зазора:

Площадь поперечного сечения:

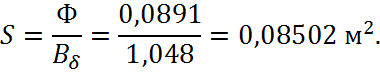
Результаты расчетов сводим в таблицу 2.

Таблица 2.

№ участка	Наименование участка	Магнитный поток, Вб	Поперечное сечение, м2	Длина, см	Индукция, Т	Напряженность магнитного поля, А/см	Магнитная напряженность участка, А
1	Зубцовый слой якоря	0,0891	0,0424	4,169	2,1	515	2147
2	Сердечник якоря	0,0445	0,0318	13,4	1,4	18,2	244
3	Зубцовый слой полюса	0,0935	0,0586	4,9	1,59	43	211
4	Сердечник полюса	0,111	0,0655	8,4	1,7	83	697
5	Стык полюса с ярмом	0,111	0,0655	0,008	1,7	—	136
6	Переход ярмо – полюс (выход)	0,111	0,09098	8,35	1,22	9,9	82,7
7	Остов (ярмо)	0,0557	0,0538	15,3	1,035	6,1	93,3
	Сумма магнитных напряжений всех стальных участков магнитной цепи
8	Воздушный зазор	0,0891	0,08502	0,7104	1,048	—	5956
	МДС для проведения магнитного потока по магнитной цепи
	МДС на компенсацию действия реакции якоря
	Полная МДС обмотки полюса