Сложное напряженное состояние: Методическое пособие по курсу сопротивления материалов, страница 4

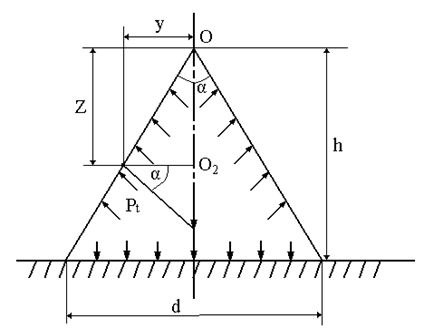
Определить                                                                      

«Меридианом» здесь является

прямая, и поэтому р_m=∞. Располагая     

начало координат в вершине конуса,                                                  

легко найдем второй главный радиус                              

кривизны поверхности конуса.                                                 

Теперь из уравнения Лапласа находим                                              

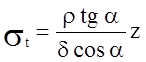Наибольшее значение напряжения  st будет z=h т.е. у основания

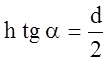конуса.

Учитывая, что

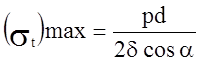Получим

         

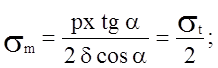Меридиональное  напряжение найдется из уравнения

Радиальное напряжение принимаем равным 0.

                                                                                                                

                    

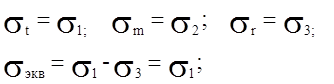4.2 ТОНКОСТЕННЫЕ ОБОЛОЧКИ , НАХОДЯЩИЕСЯ ПОД

      ДЕЙСТВИЕМ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ

          Основная теорема.

          Если на кривую поверхность действует давление жидкости, то вертикальная составляющая полной силы давления равна весу жидкости в объеме, ограниченном рассматриваемой поверхностью, вертикальные образующие которой проходят через границы рассматриваемой поверхности.

          Пример 1.Подобратьтолщину стенки резервуара, наполненного жидкостью, удельный вес которой  . Размеры резервуара            Допускаемое напряжение .

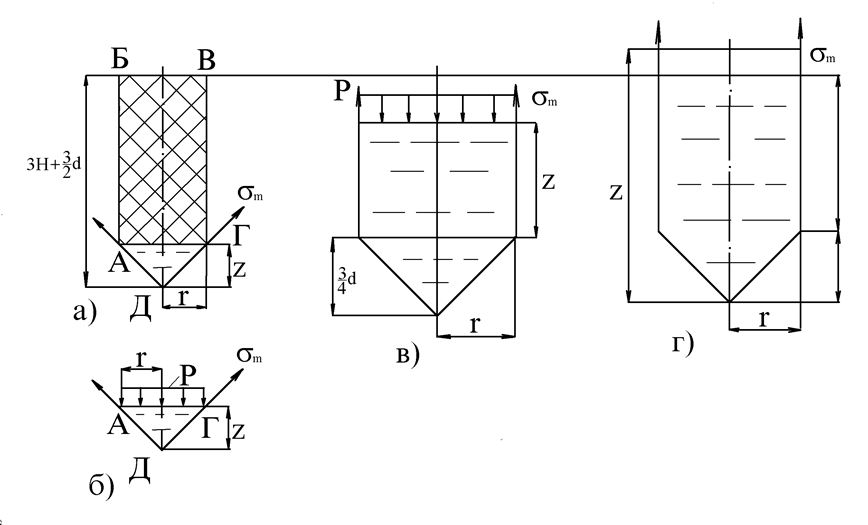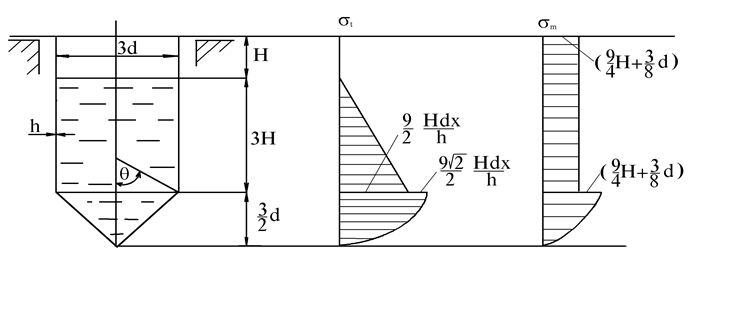
          Рассмотрим три участка. Первый участок (рис. а ,б) 0<Z1<(3/2)d: Давление 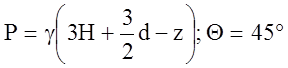, радиусы .

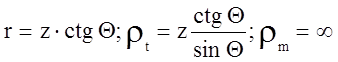Второй участок (рис. в):

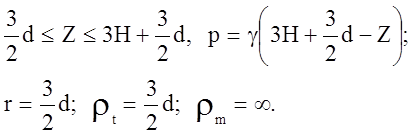
Третий участок (рис. г)

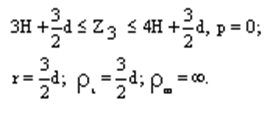На всех участках радиус кривизны , поэтому окружное напряжение   можно определить сразу из уравнения Лапласа по формуле

               

Первый участок

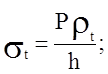
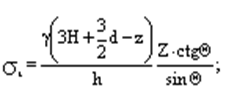Из условия 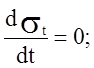 определяется координата Z^*, при которой напряжение  принимает экстремальное значение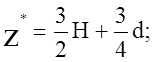

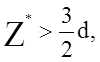 поэтому в интервале 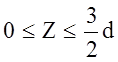 окружное напряжение  не может принимать экстремальное значение, и наибольшее напряжение будет возникать при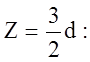

                                 .

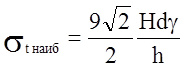Для определения меридионального напряжения на первом участке коническая поверхность резервуара рассекается коническим нормальным сечением на расстоянии Z от вершины конуса. Вертикальная составляющая сил давления жидкости равна весу жидкости, заключенной в объеме АБВГД. Для части оболочки, изображенной на рисунке (а), уравнение равновесия записывается следующим образом:

            ,

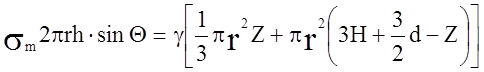откуда

            .

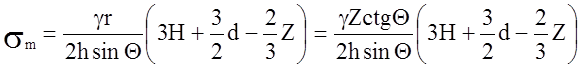Осевая составляющая сил давления жидкости могла быть определена иначе. Она складывается из веса жидкости в отсеченной части и силы давления выше расположенных слоев жидкости (рис.б).

            .

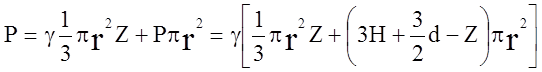 Координата 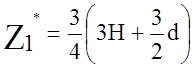, определенная из условия 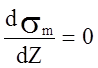, больше  и находится вне первого  участка. Наибольшее напряжение  возникает в точках, определяемых координатой ,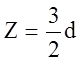

            .

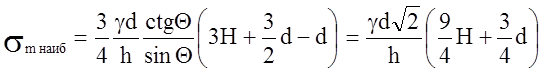Второй участок .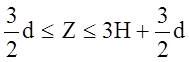

Окруженное напряжение , имеет вид

.

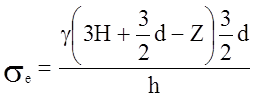При     ,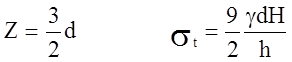

при      .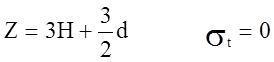

Меридиональное напряжение  определяется из условия равновесия отсеченной части оболочки. Вертикальная составляющая сил давления складывается из веса жидкости в отсеченной части и силы давления выше расположенных слоев жидкости:

,

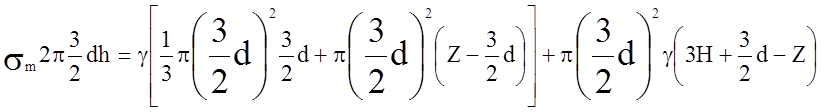откуда

               .

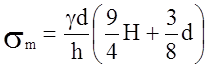Величина меридионального напряжения  не зависит от координаты Z.

Третий участок. Окружное напряжение .

          Для определения меридионального напряжения  рассматривается равновесие отсеченной части резервуара. Вертикальная составляющая сил давления равна весу всей жидкости, помещенной в сосуде,

             ,

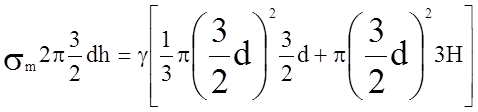тогда

             .

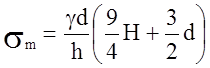Согласно выражениям , полученным ранее строятся эпюры напряжений .

          Наибольшие напряжения возникают в точках первого участка при 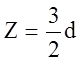. Так как напряжения  одного знака, то для точек срединной поверхности имеем:

                .

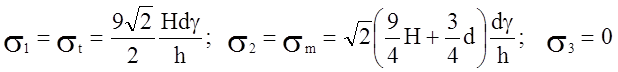Эквивалентное напряжение по гипотезе наибольших касательных напряжений .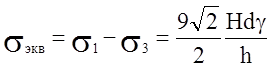

Толщина оболочки определяется из условия прочности

                      .

В этом случае

.

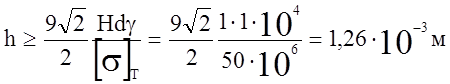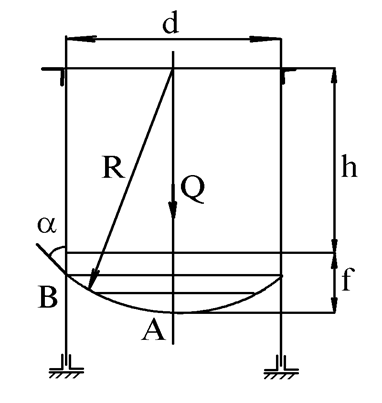
Пример 2. Расчет провесного днища и скрепляющего кольца.

          На рисунке изображен открытый цилиндрический резервуар  для хранения жидкости. Сферическое дно резервуара скрепляется с цилиндрическим корпусом с помощью специального элемента – кольца из размалкованного уголка (уголок, полки которого деформированы так, что внутренний угол между ними больше 90^○). Удельный вес жидкости -. Общий вес жидкости –Q, прочие данные указаны на рисунке. В точке А в центре днища по симметрии .

Давление жидкости здесь равно .

Находим

               .

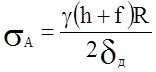Здесь  - толщина стенок.

          В точке В . Меридиональное напряжение  найдем из условия равновесия днища.

                                                  

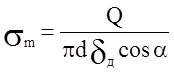
Окружное напряжение  теперь можно найти из уравнения Лапласа, учитывая, что на уровне точки В давление жидкости равно .

Отсюда

                                              .

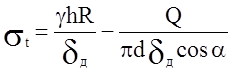Угол  и основные размеры резервуара связаны очевидным уравнением

                                                       .

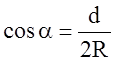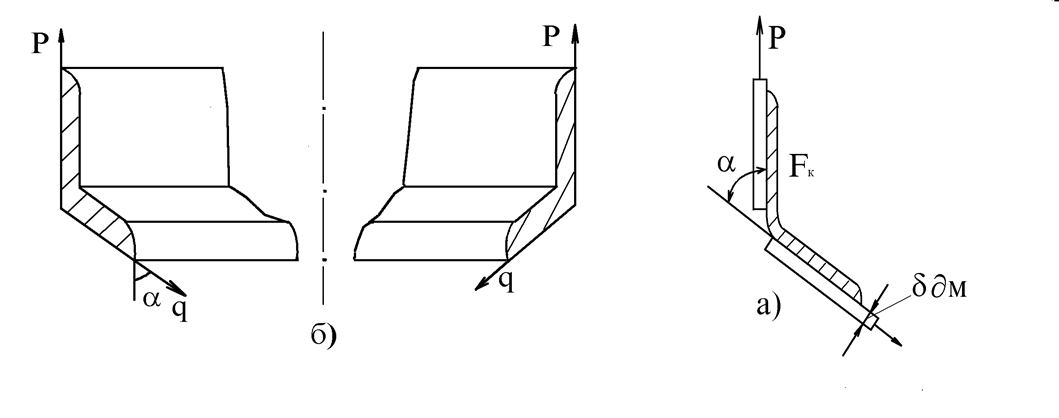
Опасной точкой при постоянной толщине днища является точка А.

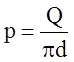 Соединительное кольцо (см. рис.) подвергается действию равномерно распределенного по вертикальной  полке погонного усилия и по наклонной полке действию равномерного погонного усилия

.

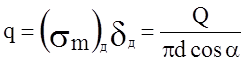          Радиальная составляющая этого усилия 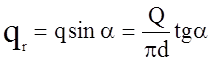 вызывает сжатие скрепляющего кольца по уравнению

или .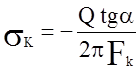

          Отсюда получается формула проверки скрепляющего кольца на сжатие (наиболее опасное действие сил на кольцо)

                                         .

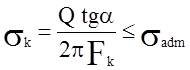Литература

1.  Филин А.П. Прикладная механика твердого деформируемого тела.-                                        М.: Машиностроение,1975.-832 с.

2.  Требушко О.И. Основы теории упругости и пластичности.- .:Наука, 1984. –319 с.

3.  Писаренко Г.С. и др. Справочник по сопротивлению материалов.- Киев.: Наук.думка, 1975.- 704 с. .

4.  Тайтур Г.К. Курс сопротивления материалов.- Минск.: Высш. школа,1964.- 216 с. .

5.  Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1986. –512 с.

     

УДК   620.10

Мосиянова Елена Ивановна

Кулибаба Виктор Васильевич

Сложное напряженное состояние

Методическое пособие

Подписано в печать                               Формат 60 84 16

Печ.л.        Усл. Печ. Л.      Уч.изд.л.       Тираж      экз.

Размножение КФ МГТУ им.Н.Э.Баумапна, ул. Гагарина,3

.