Помехоустойчивое кодирование, страница 7

Очевидно: .                                  (*)

 - должен быть кодовым многочленом, т.е. делящимся на , это левая часть выражения (*). Первое слагаемое справа также делится на , т.к. а(х) – кодовый многочлен по условию. Значит обязано делиться на  второе слагаемое, чтобы  был кодовым. Показано тем самым чтобы полиномиальный код был циклическим необходима делимость двучлена  на образующий многочлен . Достаточность следует также из (*): если () делится на , то и правая часть (*) делится на , т.е.  - кодовый многочлен.

Отсюда следует, что задавая код в качестве  можно брать только делители двучлена .  Циклические коды существуют для любого  . Сколько различных кодов длины  может быть задано зависит от значения , иначе от многообразия множителей (простых),  на которые разлагаются . При знак «-» и знак «+» для эквивалентны. Два кода находятся предельно просто, т.к. из школьного курса известна формула для суммы  членов геометрической прогрессии со знаменателем х.

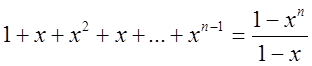, т.е.

Первый код  - это код с проверкой на четность, второй код   - это код с повторением.

Для задания циклических кодов надо уметь разлагать на простые множители двучлены .

Рассмотрим пример. Пусть нас интересуют коды длины . Разложение:  получается методом проб (в общем случае есть специальная методика разложения). Из разложения следует (см. таблицу):

(n,k)	g(x)	Примечание
(7,6)	x+1	Код с проверкой на четность
(7,5)	-	Не существует, т.к. нет g(x) второй степени
(7,4)		Код Хэмминга
(7,4)		Аналогичен по характеристикам предыдущему
(7,3)		Одинаковы по характеристикам
(7,3)
(7,2)	-	Не существует
(7,1)		Код с повторением

6.6  Разложение двучленов примитивной длины на простые множители

Длина кода называется примитивной, если , где т – целое, больше 2х. Разложение необходимо знать, чтобы задавать циклические коды оговоренной длины п. Разложение основывается на теореме Виета (см. школьный курс): если известны вещественные корни многочлена , то он равен . Если есть комплексные корни, то сохраняют многочлен большей степени, чем первая, с объединенными комплексно-сопряженными корнями.

Разложение в конечных полях проще. Основывается оно на использовании ряда теорем или свойств. Сформулируем их.

1.  Для каждого элемента поля  существует минимальный многочлен  с коэффициентами из простого подполя . Он неприводим. Минимальный многочлен называется минимальным многочленом наименьшей степени, который обращается в ноль  при , .

2.  Если  - многочлен с коэффициентами из  при , где , обращается в ноль, то  делится на .

3.  Двучлен  делится на двучлен  тогда и только тогда, когда  делится на .

4.  Все корни двучлена  есть элементы (ненулевые) поля .

5.  Мультипликативная группа поля  есть циклическая группа, т.е. существует в поле элемент, который называется примитивным и из него операцией умножения только над ним получаются все остальные элементы.

6.  Любой делитель двучлена  неприводимый над  имеет степень равную  или меньше.

7.  Цепочка корней неприводимого над  многочлена степени  получается по формуле (по правилу) , где - один из корней, т.е. , .

8.  Возведение многочлена  в степень   эквивалентно возведению в эту степень -ов в  .

9.  Теорема БЧХ. Если в цепочке корней   кода имеется последовательность 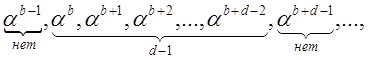 то кодовое расстояние этого кода равно  или больше. Его обозначают  и называют конструктивным кодовым расстоянием.

10.  Для любых целых положительных значений  и  существует циклический код длины , исправляющий все ошибки кратности  и меньше и содержащий не более  проверочных символов.

Рассмотрим конкретный пример.

Пусть , .

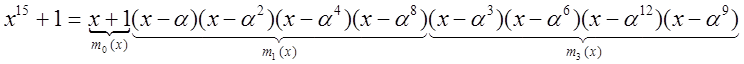
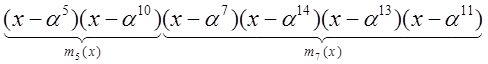
Питерсон, Уэлдон – Приложение В.

3          37       

5          7         

7,         14,       13,       11

                       

 двойственный к 1 .

6.7  Разложение двучленов непримитивной длины на простые множители

Интерес представляют длины нечетной длины и не равные . Изложим формальную процедуру решения данной задачи.

1.  Используя таблицу В.1 монографии Питерсон У., Уэлдон Э. «Коды, исправляющие ошибки» (перевод с английского – М: Мир, 1976), находим, в каком поле лежат корни разлагаемого двучлена из условия . Потребуется далее знать значение  и значение . Первый параметр указывает, в каком поле лежат корни, а  будет необходим для поиска делителей в таблице В.2.

2.  В соответствии со свойством 7 составляем все цепочки корней.

3.  Находим искомые множители в списке найденного значения степени  таблицы В.2 по алгоритму – корню  будет соответствовать у непримитивной длины корень , его мы и находим из таблицы.

Проиллюстрируем процедуру разложения на конкретном примере. Пусть . Разложитьна простые множители.

1. 

.

2. 

Из цепочек корней заключаем, что есть два многочлена 12-й степени, один многочлен четвертой степени, два многочлена третьей степени и один многочлен первой степени.

3.  Находим многочлены.

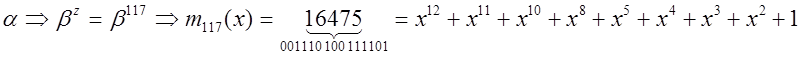
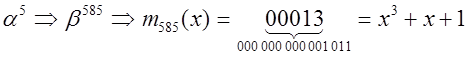
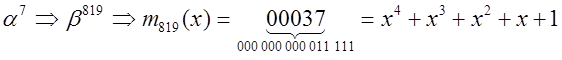
Таким образом, получается:

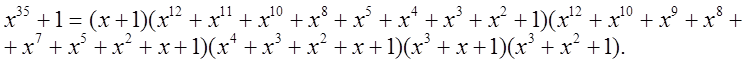
Имея разложение и последовательности корней, легко конструируется код с требуемым кодовым расстоянием. Для этого строят цепочку корней нужной по свойству 9 длины. При объединении последовательностей корней надо стремиться к минимуму избыточных символов. Следует помнить еще одну особенность, то, что 1=a⁰=aⁿ и свойство цикличности.