Помехоустойчивое кодирование, страница 5

Доказательство. Пусть матрица Н обладает свойст­вом, что  столбцов линейно независимы,  - кодовый вектор. Тогда  или, раскрыв матричную запись, получим 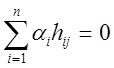. Число элементов  (т.е. столбцов Н), реально участвующих в проверках, очевидно, равно числу ненулевых компонент вектора , т.е. весу кодового вектора. В силу условия линейной не­зависимости  столбцов матрицы Н равенство нулю возможно только при d или большем числе ненулевых ;. Значит, минимальный вес ко­дового вектора равен d  или больше и кодовое расстояние тоже d или больше. Теорема доказана.

Можно, как следствие, заметить, что если все столбцы матрицы Н различны, то кодовое расстояние равно трем или больше. Действитель­но, при всех различных столбцах никакие два из них в сумме не равны нулю, т.е. линейно независимы. Отсюда .

2. Если имеется модулярное представление кода, в частности дво­ичного, то спектр этого кода можно найти на основании теоремы Макдональда.

Веса каждого из  ненулевых кодовых слов двоичного группового кода могут быть найдены как компоненты вектора, получающегося в результате матричного умножения (как матриц с действительными чис­лами) вектора  модулярного представления кода на матрицу  :  или . Веса кодовых слов оказываются упорядо­ченными так же, как кодовые слова в матрице .

3. Граница Синглтона. Минимальный вес любого линейного -кода удовлетворяет неравенству .

Доказательство. Ненулевое слово минимального веса имеет вес d. Имеются слова в систематическом коде о одним ненулевым информационным символом. Так как еще имеется только провероч­ных символов в слове, то вес не может быть больше . Код с  называется кодом с максимальным расстоянием.

4. Спектры линейного кода А и двойственного ему  взаимосвя­заны. Эта связь оказалась весьма полезной для расчета спектров многих блоковых кодов. Пусть  - спектральная функция -кода А,  - спектральная функция . Согласно тождеству Мак-Вильямс:

                                                    (*)

Спектры кодов до  в настоящее время находятся с помощью ЭВМ. С помощью (*) удается найти спектр кода большей длины, лишь бы число проверочных символов не превышало 25.

Методы декодирования линейных кодов

Декодирование по максимуму правдоподобия является наиболее об­щим методом. Для симметрично искажающих каналов без памяти декодиро­вание заключается в последовательном сравнении принятой последова­тельности с каждым из возможных кодовых слов и выборе среди них ближайшего по метрике Хемминга в качестве результата декодирования. Чтобы реализовать этот метод, целесообразно построить таблицу стандартной расстановки. Как эта таблица получается, проще всего пояс­нить на примере группового кода, код в этом случае есть подгруппа. Элементы подгруппы - кодовые комбинации. Их запишем в первую строку таблицы, поместив нулевую комбинацию в начало, и разложим группу по смежным классам. Все возможные на приеме последовательности будут содержаться в таблице.

Лидеры смежных классов		.			…
		.			…
		.			…
	Смежный класс
		.			…
		.			…

Каждая строка образует смежный класс. Первый элемент строки называют лидером смежного класса (образующим). Если в качестве лидеров выбра­ны элементы строки с минимальным весом, то приведенная таблица назы­вается стандартной расстановкой. Весом смежного класса считают вес его лидера.

Пусть а - переданное слово; - принятая последовательность. Если используется ДСК без памяти, то в качестве лидеров надо выбирать векторы ошибок наиболее вероятные, т.е. с одиночной ошибкой, двойной и т.д., пока позволяют свойства кода. Декодирование будет состоять в следующем:

-  находится в таблице последовательность, равная ;

-  определяется лидер той строки, в которой оказалась последовательность ;

-  вычисляется  как результат декодирования.

Ценность стандартной расстановки относительна. Для больших  и  технически реализовать такую таблицу на ЭВМ становится невозмож­ным. Трудность табличного декодирования была отмечена в главе I. Это не означает полного отрицания метода декодирования по максимуму правдоподобия. Обычно за счет дополнительной информации о достовер­ности символов удается ограничить "объем пространства" просматривае­мых комбинаций. Типичным примером являются алгоритмы Чейза [13].

6.4.3  Синдромное декодирование

Синдромом вектора  называет вектор , где  - проверочная матрица. Если а - кодовый вектор, то, очевидно, . Утверждается, что все векторы, принадле­жащие одному смежному классу, имеют совпадающие синдромы. Действительно, если

 и - векторы одного смежного класса с образующим, равным , то , , т.е. .

Синдромы разных смежных классов различны. Декодирование будет состоять в вы­числений синдрома ; нахождении в памяти лидера, соответст­вующего этому синдрому, выдачи результата декодирования в виде .

С помощью синдромов можно различать ошибки с точностью до смежных классов, которые они образуют.

Техническая реализация этого способа проще, чем по максимуму правдоподобия, но все еще достаточно сложна. Оценим и сравним сложность аппаратной реализация кодирования и декодирования двоичным кодом по максимуму правдоподобия и синдромному. Сложность будем оценивать в первом приближении числом элементов, из которых состоит ко­дер ила декодер, считая ах однородными.