Исследование функций. Приложение производной, страница 15

f (x₀ )> f (x)                             (6.1)

Рассмотрим выражение

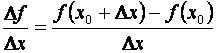,                       (6.2)

которое при является производной функции в точке x₀. Зафиксируем Dx таким образом, чтобы x₀+Dx принадлежащему интервалу (x₀-d, x₀+d).   Величина        f (x₀ + Dx) - f (x₀ ) в силу соотношения      всегда отрицательна. Следовательно, знак выражения, определяемого равенством (6.2), полностью определяется знаком .

А именно: при Dx > 0

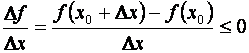                           (6.3)

при

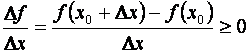                           (6.4)

Переходя к пределу в (6.3) и (6.4) получим производную . Из (6.3) вытекает, что f¢ (x₀) £ 0, а из (6.4)   -         f¢ (x₀) ³ 0, а это означает, что f¢ (x₀)= 0. В этом и состоит необходимое условие экстремума. Экстремум будем искать только в тех точках, где производная равна нулю. Такие точки называются стационарными. Особо следует отметить, что равенство нулю производной вовсе не означает, что в этой точке функция достигает экстремума. Это условие, подчеркнем еще раз, является необходимым, но не достаточным. Например, функция x³ имеет производную 3x², равную нулю при x= 0, но в этой точке функция не имеет экстремума она все время возрастает.

Рассмотрим класс рассматриваемых функций и допустим, что в отдельных точках  интервала (a, b) функция не имеет производных, тогда не исключена возможность, что именно в этих точках функция может иметь экстремум. Например, функция    имеет в точке x= 0 минимум, хотя производной в этой точке функция не имеет. Правая производная равна +1, левая -1. Суммируя все вышесказанное, сформулируем необходимое условие экстремума функции.