Другие предметы \ Моделирование систем управления

Разработка динамической модели гидравлической системы. Моделирование и анализ статического состояния гидросистемы, страница 4

В системе уравнений (25), нелинейной является функция , для них частные производные имеют вид:

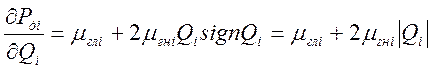
Тогда матрица Якоби, исследуемой гидросистемы, имеет вид:

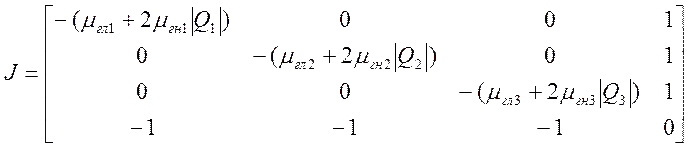
Подставим цифровые значения в матрицу Якоби:

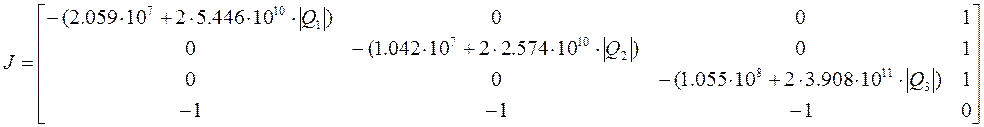
3.3 Решение систем уравнений статической модели методом Ньютона

Из различных численных методов, систем алгебраических уравнений используем метод Ньютона, который обладает наибольшей скоростью сходимости. Алгоритм включает следующие этапы:

1) выбор начального приближения

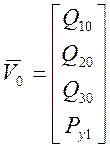
2) вычисление матрицы Якоби в точке

3) вычисление вектора невязок , исходной системы алгебраических уравнений:

4) Определение вектора поправок  по формуле:

5) Определение нового приближения вектора искомых фазовых переменных, по формуле:

6) Вычисление нормы вектора невязок:

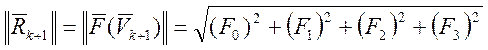
7) Проверка условий окончания итерационного процесса

При выполнении условия, процессы останавливаются, и в качестве точки расширения применяется вектор , иначе осуществляется переход и итерация продолжается.

Расчет произведен с помощью Matcad и представлении в приложении.

В таблице представлены результаты при двух значениях подачи насоса

      Таблица 4 – Результаты статического анализа

  Фазовые координаты

4 Моделирование и анализ переходных процессов

Для технической системы, наиболее характерны функционирующие в условиях непрерывно изменяющихся внешних воздействий. Состояние системы при этом оказывается неустановивившимся. Это состояние характеризуется изменением во времени фазовых координат системы. Такой режим работы называется динамическим, и он описывается дифференциальным уравнением. В общем, случаи математическая модель представляет собой систему обыкновенных дифиренциальных уравнений вида:

где,  - вектор фазовых координат системы;

 - вектор производных фазовых координат по t;

 - вектор внешних воздействий. 

В зависимости от характера изменения воздействия  и описания внутренних физических свойств системы, ее модель может быть детерминированной или вероятной. Функциональное проектирование технической системы на основе модельных режимов, в число которых входит переходный процесс – переходный процесс системы называется переход системы из одного установившегося состояния в другое. Моделирование переходного процесса позволяет исследовать быстродействие, точность, динамичность, колебательность и другие свойства системы.

Решение задач анализа переходного процесса, включает три этапа:

1) Интегрирование системы дифференциального уравнения.

2) Определение показателей качества.

3) Оценка степени выполнения технических требований к системе.

4.1 Формирование матрицы Якоби в динамической модели

Матрица динамической модели составляется аналогично статической. В общем случаи система дифференциальных уравнений:

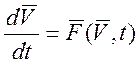
где,

A  -  матрица Якоби;

 - вектор фазовых координат ;

 - вектор функции внешних воздействий .

С учетом ранее произведенных расчетов, запишем систему дифференциальных уравнений, характеризующую динамическую модель гидроситемы:

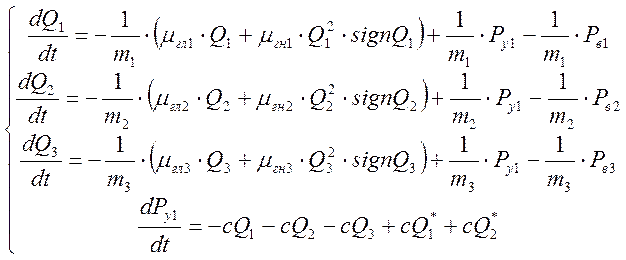
Так как система дифференциальных уравнений нелинейная, то элементами матрицы Якоби, являются частные производные по фазовым координатам:

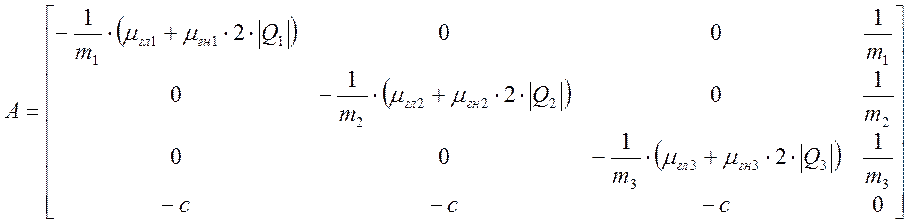
Матрица Якоби в динамическом случаи переменная, ее элементы зависят от фазовых координат системы -  расходов жидкости .

4.2 Выбор параметров интегрирования

Переходную характеристику определяют по средствам дифференциального уравнения, для чего необходимо провести выбор параметров.

Пусть переходный процесс оценивается, как реакция системы находящейся в состоянии покоя на ступенчатом воздействии вида:

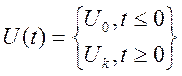
где, U0  и Uk – начальное и конечное значение функции воздействия U(t), причем:

U0=const, Uk=const,

Определим   и при  , значения фазовых координат, определены при анализе статического состояния:

Начальное значение:

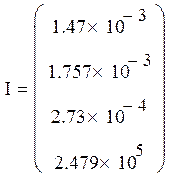
Конечное значение:

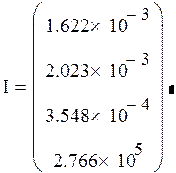
Если система устойчива, то через некоторый период времени, система перейдет из одного состояния V0 в Vk , в противном случае конечных значений не достигнет.

Вектор входных воздействий при  имеем:

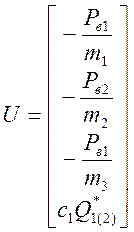
Для численного интегрирования, будем использовать неявный метод Эйлера, выбор шага интегрирования для которого h осуществляется исходя из условия устойчивости метода (устойчивости системы):

где, h – шаг интегрирования;

собственное значение матрицы Якоби.

Для комплексных значений , условие устойчивости имеет вид:

Собственными значениями матрицы Якоби порядка n – называют корни , где k =, ее характеристическое уравнение , где Е – единичная матрица.

Произведем расчет значений матрицы Якоби с учетом начальных значений расходов:

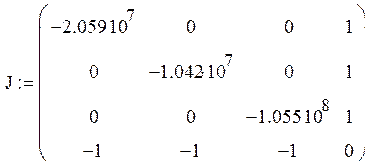
Запишем единичную матрицу:

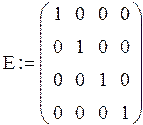
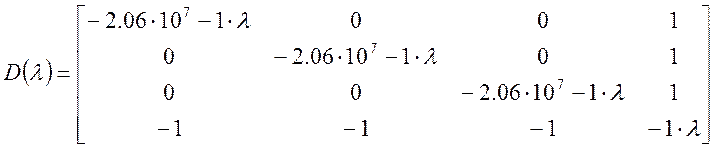
Тогда характеристическое уравнение имеет вид:

Вычислив корни характеристического уравнения, найдем собственное значение матрицы Якоби:

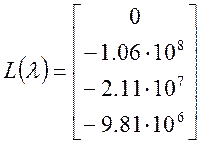
Все корни характеристического уравнения имеют отрицательные действительные части, что говорит об устойчивости самой системы. Отсутствие комплексно – сопряженных дает монотонный процесс ряда фазовых координат. Рекомендуемый шаг интегрирования равный h=0.5. Выполним проверку устойчивости, методом Эйлера при данном шаге:    

Следовательно, шаг h=0.5 обеспечит, устойчивость метода, то есть приемлемую точность вычислений.

Скачать файл