Основы теории четырехполюсников, страница 6

На частоте f=1кГц цепь длины l=30÷40км., является цепью с распределенными параметрами. А на частоте f=1ГГц цепь длиной l=2÷3мм., также является цепью с распределенными параметрами.

Примерами цепей с распределенными параметрами являются

-воздушно-двухпроводная линия;

-электрический кабель;

-коаксиальный кабель;

-полосковая линия, прямоугольный или круглый волновод и т.д.

Цепи с распределенными параметрами часто называют длинными линиями.

9.1. Понятие о длинной линии и распространение волн в ней

Рассмотрим воздушную двухпроводную линию, длина которой соизмерима или больше длины электромагнитной волны (рис.9.1а). При протекании тока по проводам вокруг них возникает магнитное поле Н, что свидетельствует о наличии индуктивности, распределенной вдоль линии. Между проводами возникает электрическое поле, что говорит о емкости. Провода и диэлектрик между проводами нагреваются, что свидетельствует о наличие потерь, т.е. говорит о сопротивлении.

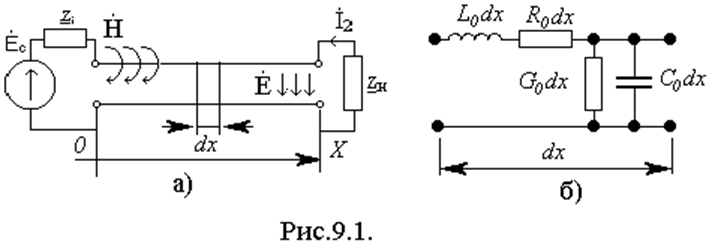Количественно физические параметры длинной линии характеризуются следующими погонными параметрами, т.е. параметры, приходящие на единицу длины:

L₀- погонная индуктивность. Определяется как индуктивность короткозамкнутого отрезка линии длиной 1 метр. Единица измерения - [Гн/м].

R₀- погонное сопротивление. Определяется как сопротивление короткозамкнутого отрезка проводов длиной 1 метр. Единица измерения - [Ом/м].

C₀- погонная емкость. Определяется как емкость между проводами разомкнутого на конце отрезка линии длиной 1 метр. Единица измерения - [Ф/м].

G₀- поперечная проводимость. Определяется как проводимость между проводами разомкнутыми на конце отрезка линии длиной 1 метр. Единица измерения - [См/м].

Выделим участок длины dx. Его можно представить эквивалентной схемой приведенной на рис.9.1б.

Если погонные параметры не зависят от x, то линии называются однородными, если погонные параметры зависят от координаты х, то – неоднородными. Если R₀=G₀=0, то линию называют линией без потерь.

Составим уравнения, позволяющие определить напряжение и ток в любом сечении длинной линии, для длинной линии без потерь (рис.9.2). Запишем выражения относительно приращений напряжения и тока

                                               (1)

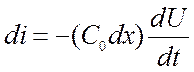                                               (2)

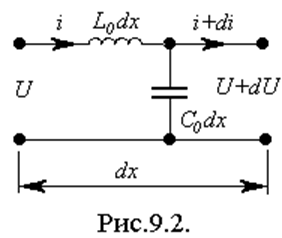Поделим первое и второе уравнение на dx, а затем подифференцируем первое уравнение по х, а второе по t, а затем выразим смешанные производные:

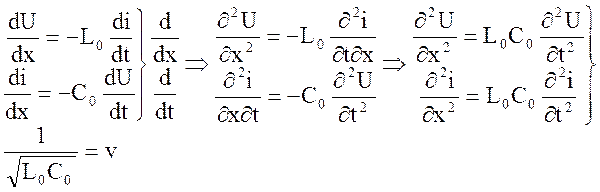
Полученные (крайние справа) уравнения, для линии без потерь, называются волновыми.

Уравнение, полученное аналогично, но с учетом R и G, для линий с потерями, называются телеграфными. Они записываются так

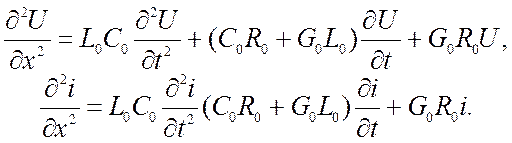В общем случае, решение волновых уравнений можно представить выражениями:

,

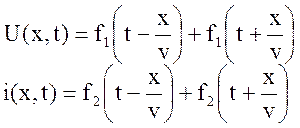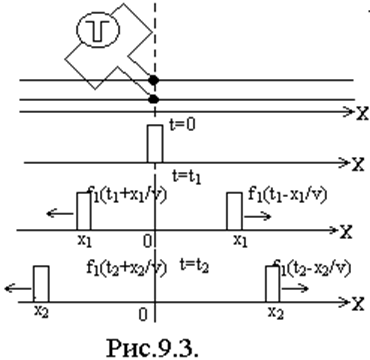
где функций f₁ и f₂ зависят от начальных и граничных условий, т.е. от сигналов, которые подводятся к длинной линии, но главное эти функции должны быть дважды дифференцируемыми.

Первое слагаемое называется прямая волна, а второе – обратная волна. С физической точки зрения прямая волна характеризует сигнал, который распространяется в направлении х, а обратная волна – сигнал которые распространяется вдоль линии в противоположном направлении (см. рис.9.3).

9.2. Полубесконечная длинная линия

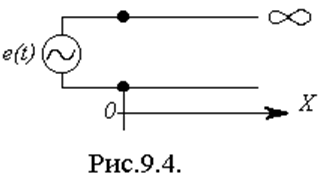
Решение волновых уравнений значительно упрощается, если рассматривать полубесконечную длинную линию при гармоническом воздействии e(t)=E_mcosωt (рис.9.4). В такой линии нет условий для распространения обратной волны, а потому существует лишь прямая, ее называют падающая волна.

Установившиеся процессы в таком линии в произвольном сечении являются гармоническими, но появляется фазовый сдвиг, который связан с конечной скоростью распространения волны. Напряжение и ток в любом сечение определяются из соотношений

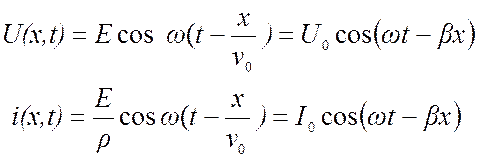
где v₀ = λ/Т = (L₀C₀)^-2  - скорость распространения сигнала в длинной линии;

β=ω/v₀ – коэффициент фазы, он характеризует фазовый сдвиг волны на единицу длины линии, иногда его называют пространственная частота сигнала т.к. β= 2π/λ , где λ – длина волны (это название дано по аналогии с тем, что ω= 2π/Т – временная частота),

Отношение комплексной амплитуды напряжения к комплексной амплитуде тока прямой волны называют волновым сопротивлением. Волновое сопротивление линии без потерь имеет чисто резистивный характер . Иногда ρ называют характеристическим сопротивлением.

Эти три параметра (v₀, β, Zв) называются волновыми или вторичными параметрами длинной линии.

Таким образом, в длинной линии без потерь сигнал в любом сечении не изменяет своей формы и амплитуды, но наблюдается запаздывание за счет конечной скорости распространения. В линии с потерями наблюдается не только запаздывание во времени, но и затухание сигнала по амплитуды с возрастанием х.

9.3. Линия конечной длины. Отражения

На практике часто используются линии конечной длины. Пусть однородная линия длиной l нагружена на конце (x=l) на сопротивление Z_н. В начале, при x=0, линия питается от генератора гармонической ЭДС с внутренним сопротивлением R_i. Волновое сопротивление линии Zв = r.

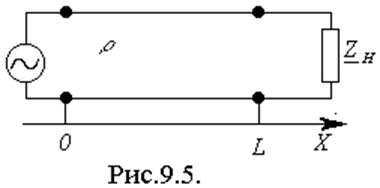В установившемся режиме в линии присутствуют 2 волны. Эти волны распространяются в двух взаимнопротивоположных направлениях. Волна, движущаяся от генератора к нагрузки, называется прямой или падающей. Волна, движущаяся от нагрузки к генератору, называется обратной, или отраженной. Появление обратной волны связано с отражением падающей волны от нагрузки. Таким образом, в длинной линии в каждый момент времени, в каждой точки сечения присутствуют алгебраическая сумма двух волн - падающей и отраженной.

При гармоническом мгновенное значение напряжения в любой точке определяется суммой падающей и отраженной волн напряжения, а мгновенные значения тока  - разностью падающей и отраженной волн тока. Знаки в суммах связаны с тем, что положительные направления напряжений U_пад, U_отр выбраны одинаково (сверху вниз), а у токов I_пад, I_отр -  встречно, поэтому они вычитаются

U_(x,t)=U_пад+ U_отр,