Математическое описание сигналов различного типа. Разложение сигнала по системе ортогональных и ортонормальных функций. Интеграл Фурье. Разложение функции в ряд Лорана, страница 5

В предельном случае эти ограничения могут быть сведены к ограничениям, накладываемым на отдельные выходные величины. При решении задач оптимизации объект управления можно описать с помощью некоторого оператора :

 - выходная величина объекта.

Чаще всего описание объекта задается с помощью системы дифференциальных уравнений.

Для решения уравнений необходимо задать граничные условия при t=0 и конечное состояние объекта управления G. В этом случае задача синтеза будет иметь следующий вид.

По заданному систематическому описанию объекта (в виде дифференциальных уравнений), граничными условиями (при t=0), ограничением вида [2]; внешнего воздействия Х и критерия оптимизации [1], а также устройству управления, обеспечивающего такое оптимальное управление при котором достигается цель управления при максимальном либо минимальном значении параметра оптимизации и выполнении всех ограничений.

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ.

Принцип максимума Понтрягина.

 

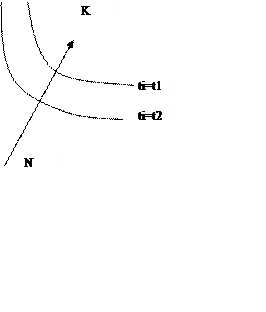
Перевести за минимальное время изображающую точку из некоторого начального положения N в определенную конечную точку К.

Каждой точке фазового пространства окружающего точку К, соответствует оптимальная траектория и соответствующее ей минимальное время перехода в эту точку. Вокруг точки К можно построить поверхности, являющиеся геометрическим местом точек с одинаковым минимальным временем ti перехода в эту точку.

Эти поверхности называются изохронами. Оптимальная по быстродействию траектория из точки N в точку К должна быть максимально близка к нормалям насколько это позволяют ограничения, наложенные на величины управления. Движения вдоль изохрон увеличивает время процесса, так как приводит к дополнительным затратам времени на движение не уменьшающее расстояние до конечной точки, то есть на всей траектории произведение вектора скорости изменения выходной величины 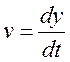  на вектор, обратный градиенту времени перехода в конечную точку   должен быть максимальным, то есть должно выполняться условие равенства:

 

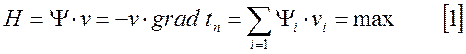
Для любого критерия оптимальности поверхности постоянного значения будут называться изоповерхностями и будет выполняться условие [1]. При практическом определении оптимального управления и оптимальной траектории изоповерхности не определяют, а находят вектора   с помощью сопряженных уравнений:

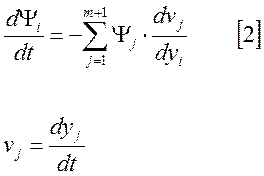
Обозначим сумму произведений:

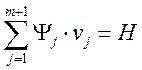
Определим производную:

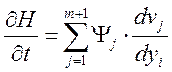
Подставим полученное значение в [2].

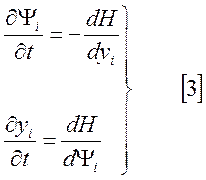
Полученное выражение называется уравнениями Гамильтона, а Н - гамильтонианом. В итоге задача сводится к следующему: определить закон управления  , дающее в результате совместного решения уравнения объекта и сопряженных уравнений такую траекторию I(t), для которой гамильтониан Н во всех ее максимумах будет иметь максимальное значение, то есть будет выполняться равенство:

 

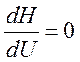
   Однако в этом случае необходимо начальное условие  и задавая для него произвольные значения, находим траекторию, которая близка к оптимальной, и последовательно приближая ее, получаем оптимальную траекторию.

 Метод динамического программирования.

Этот метод используется для определения оптимального уравнения, удовлетворяющего заданному критерию оптимизации и ограничениями, накладываемыми на управление и выходную величину исследуемой системы.

Рассмотрим некоторую цифровую систему. Пусть требуется найти некоторое управление  , заданное объектом, которое переводит данный объект из состояния характеризующийся точкой   в состояние, характеризующееся точкой .  - время переходного процесса. Критерий оптимизации для цифровой системы будет иметь следующий вид:

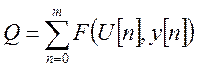
Объект управления  может быть записан с помощью конечно разностных уравнений. Задача заключается в том, чтобы найти управление U[n] в последовательности управлений:

Задача решается при движении от управления U[m-1] к U[0]. При определении управления U[m-1] для каждого из возможных дискретных значений выходного сигнала y[m-1] находи значение U (методом перебора). Одновременно определяем приращение параметров оптимизации. Из найденных управлений, определяем оптимальное, удовлетворяющее всем ограничениям, накладываемых на управление и выходные величины. Повторяем процесс до тех пор, пока не дойдем до точки, характеризующий процесс в точке y[0]. В результате получаем множество управлений, а также определяем все состояния объекта и значения критерия оптимизации.

Метод динамического программирования может использоваться для решения задач оптимизации непрерывных систем, которые предварительно подвергаются дискретизации.

Симплекс метод.

Этот метод используется при решении задач линейной оптимизации. Рассмотрим некоторые параметры оптимизации.

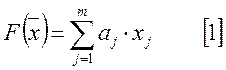
 - функция цели, стремящаяся к максимуму, либо к минимуму. На функцию  накладывается ограничение вида:

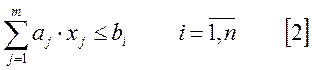 - если к максимуму.

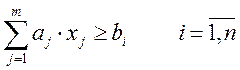 - если к минимуму.

Часто в задачах линейной оптимизации на переменную  накладываются ограничения:

 - целочисленное

Если ограничение не наложено, то задача сводится к обычной задачи линейной оптимизации. Если n<m, то на все  накладываются ограничения [4] и задача называется частично целочисленная. Если n=m, то задача называется целочисленной задачей линейной оптимизации.

На первом этапе решения задачи линейной оптимизации записывается неравенство [2], которое сводится к неравенству с фиктивными переменными. В результате получаем:

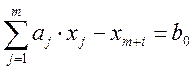
После этого определяем некоторое начальное базисное решение.

Базис – это набор любых n переменных, для которых определитель, составленный из коэффициентов при переменной, отличен от 0. Оставшиеся n-m переменные называются свободными.

 Чаще всего в качестве базисных переменных используются фиктивные переменные. Выбранные базисные переменные выражаются через свободные, и решается полученная система уравнений. Если некоторые из базисных переменных отрицательны, то полученное решение является недопустимым и необходимо перейти к новому базису. Если полученное базисное решение неотрицательно, то они являются допустимыми и их следует проверить на достижение максимума или минимума целевой функцией [1]. Если функция цели неоптимальна, то следует перейти к новому решению. Для этого одну из свободных переменных входящих в целевую функцию со знаком плюс (при определении максимума) переводят в базисную, а свободную переменную переводят в одну из базисных переменных, которая раньше других превращается в 0 и так далее до тех пор, пока функция цели не достигнет оптимального значения.

Вопросы для самоконтроля.

1.  Назовите пути построения оптимальных систем.

2.  Как выглядят условия накладываемые на процесс при оптимизации.

3.  В чем суть принципа максимума Понтрягина.

4.  Что такое Гамильтониан.

5.  В чем суть метода динамического программирования.

6.  В чем суть симплекс-метода.