Математическое описание сигналов различного типа. Разложение сигнала по системе ортогональных и ортонормальных функций. Интеграл Фурье. Разложение функции в ряд Лорана

Балаковский институт техники, технологии и управления (филиал)

ГОУ ВПО Саратовский государственный технический университет

Факультет инженерно-строительный

ЛЕКЦИИ

по дисциплине «МОТС»

специальности 220201.65-Управление и информатика в технических системах

для студентов очной формы обучения

Автор: к.т.н. доцент Ефремова Т.А.

2010 г.

Лекции по МОТС.

Содержание за 2 семестр.

2 семестр. 1

Математическое описание сигналов различного типа. Разложение сигнала по системе ортогональных и ортонормальных функций. 1

Разложение периодической функции в ряд Фурье. 3

Определение коэффициентов ряда Фурье. 5

Частный случай ряда Фурье. 7

Нахождение коэффициентов ряда Фурье от произвольной функции  с симметричными пределами. 7

Частные случаи ряда Фурье. 9

Комплексная форма ряда Фурье. 12

Интеграл Фурье. 13

Частный случай интеграла Фурье. 15

Комплексная форма интеграла Фурье. 16

Комплексные числа и действия над ними. 17

Спектры. 19

Спектральные характеристики, зависящие от времени. 21

Свойства непрерывного спектра. (Свойства преобразований Фурье). 22

Разложение функции в ряд Лорана. 25

Свойства рядов Лорана. 28

Классификация изолированных особых точек. 28

Вычет функции в особой точке. 30

Поведение функции в окрестностях бесконечно удаленной точки. 33

Пример: 35

Применение вычетов. 35

Оптимальное управление. 37

Пути построения оптимальных систем. 37

Методы решения задач оптимизации. 39

1). Принцип максимума Понтрягина. 39

2). Метод динамического программирования. 41

3). Симплекс метод. 42

ЛЕКЦИЯ 1

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СИГНАЛОВ РАЗЛИЧНОГО ТИПА. РАЗЛОЖЕНИЕ СИГНАЛА ПО СИСТЕМЕ ОРТОГОНАЛЬНЫХ И ОРТОНОРМАЛЬНЫХ ФУНКЦИЙ. РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ФУРЬЕ.

Цель. Изучить математическое описание сигналов. Рассмотреть алгоритм разложения периодической функции в ряд Фурье.

Задачи:

Изучить разложение сигналов в ряд по ортогональным и ортонормальным функциям.

Изучить разложение в ряд Фурье для периодической функции.

Изучить разложение в ряд для непериодической функции.

Изучить разложение функции на произвольном промежутке.

Функции  и  называются ортогональными, если интеграл от их произведения равен нулю.

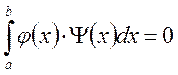
Рассмотрим ряд функций: . Система функций  называется ортогональной, если на отрезке от "а" до "b" все функции попарно ортогональны.

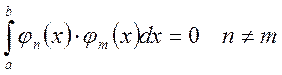
Рассмотрим промежуток где n=m:

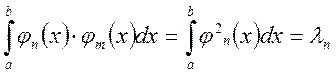
Если система функций  при n=m имеет коэффициент , то эта функция является ортонормальной. Если ортогональная система функций не ортонормальна, то ее можно получить, произведя замену:

.

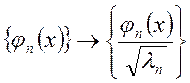Рассмотрим систему ортогональных функций  и некоторой произвольной функции . Разложим функцию  в ряд по системе ортогональных функций, то есть предположим, что существует разложение вида:

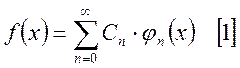
Определим коэффициенты ряда. Для этого умножим обе части равенства [1] на  и проинтегрируем. В результате получим:

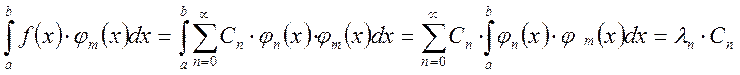
Так как система функций ортогональна и ортонормальна, то получили равенство . Выразим С_n из уравнения:

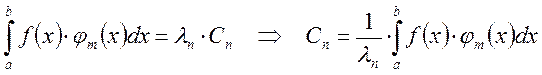
Ряд [1] называется обобщенным рядом Фурье,  - коэффициентом ряда Фурье. Ряд [1] существует тогда и только тогда, когда  является периодической функцией, а система функций  - является равномерно сходящейся.

Разложение периодической функции в ряд Фурье.

Функция   называется периодической с некоторым периодом T>0, если значение функции в точке  равно значению функции в точке t:

Для периодической функции выполняется следующее равенство:

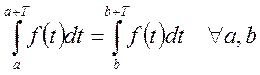
Рассмотрим гармонический процесс вида:

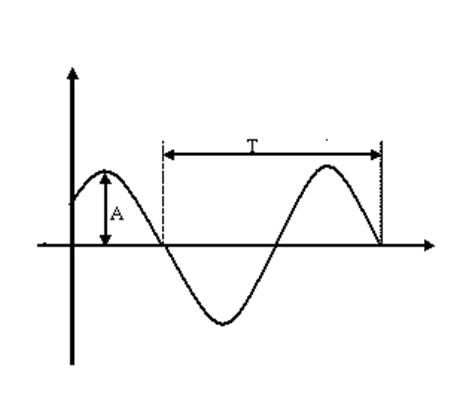
рисунок 1

, где

Рассмотрим функции:

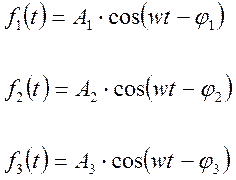
Сумма этих функций приводит к образованию некоторой новой функции с периодом Т.

.

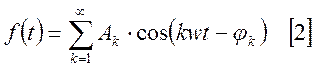Теорема.

Функция , представляющая собой сумму бесконечного ряда, является периодической и ее период совпадает с периодом Т первой гармоники. Частоты соседних гармоник отличаются на величину .

Доказательство.

Обозначим приращение частоты при переходе от  к  гармоники через , тогда для [2] получим:

.

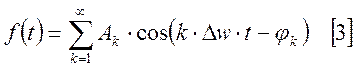Общий член ряда [3]  называется -ой гармоникой ряда. Частота  - называется частотой -ой гармоники.

Представим некоторую функцию в виде суммы гармонических функций и предположим, что существует нулевая гармоника А₀.

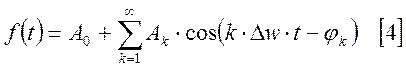
Распишем косинус разности:

Тогда для -ой гармоники:

Обозначим:

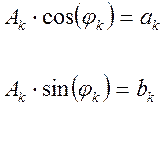
Тогда:

Обозначим:

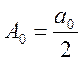
Тогда [4] примет вид:

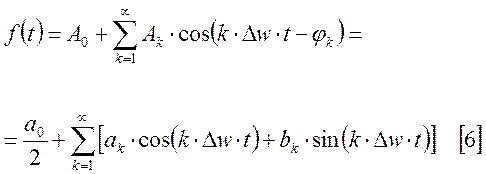
Это тригонометрическая форма ряда Фурье. Если , то 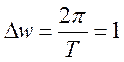. В таком случае для периодической функции с периодом  ряд Фурье будет иметь следующий вид:

Определение коэффициентов ряда Фурье.

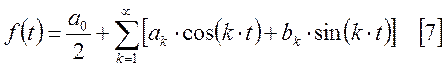
Для разложения в ряд Фурье периодических функций с периодом  используется ряд ортогональных функций следующего вида:

.

Проинтегрируем [7] на промежутке .

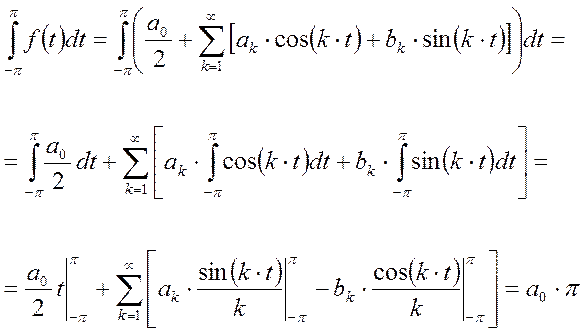
Выразим а₀.

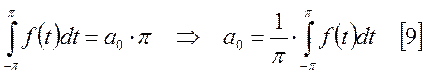
Определим  и . Для этого [7] умножим на . В результате получим:

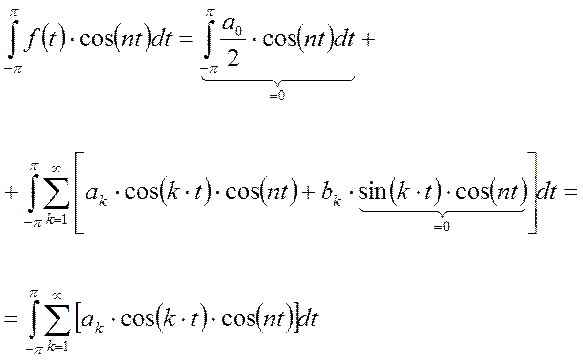
Так как система функций [8] ортогональна , то:

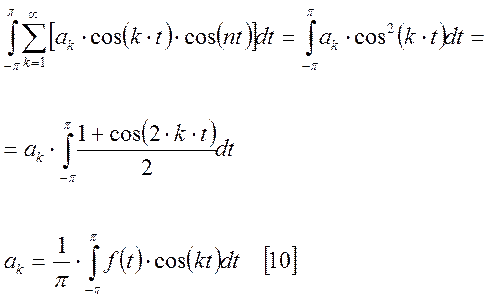
Для определения коэффициента ,  [7] умножим на . В результате получим:

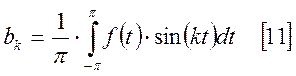
Формулы [9], [10], [11] являются формулами для определения коэффициентов ряда Фурье. Зная их можно найти амплитуду и начальную фазу k-ой гармрмоники:

Частный случай ряда Фурье.

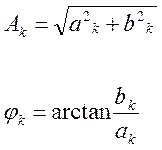
Допустим функция  на промежутке  является нечетной, тогда:

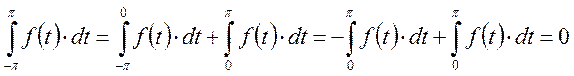
Интеграл от нечетной функции в симметричных пределах равен нулю.

Допустим функция  на промежутке  является четной, тогда:

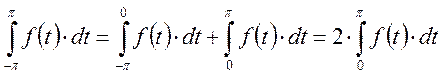
Интеграл от нечетной функции в симметричных пределах равен удвоенному интегралу в пределах, равных половине симметричной области.

Нахождение коэффициентов ряда Фурье от произвольной функции  с симметричными пределами.

Допустим функция  является четной, тогда интеграл имеет вид:

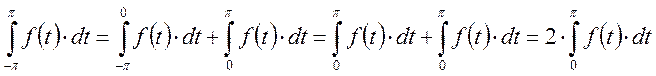
Если:

 

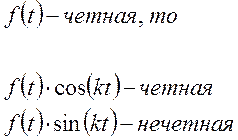
Найдем коэффициенты ряда Фурье:

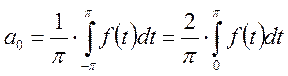
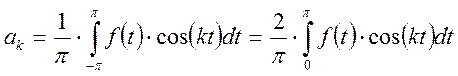
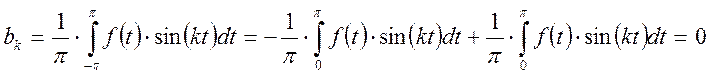
Ряд Фурье для четной функции имеет вид:

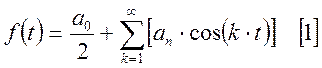
Допустим функция  является нечетной, тогда интеграл имеет вид:

 

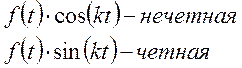
Найдем коэффициенты ряда Фурье для этого случая:

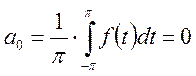
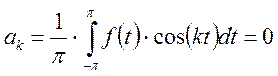
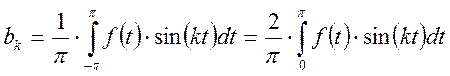
Ряд Фурье для этого случая имеет вид:

Частные случаи ряда Фурье.

Рассмотрим 4 частных случая ряда Фурье:

1.  Непериодическая функция.

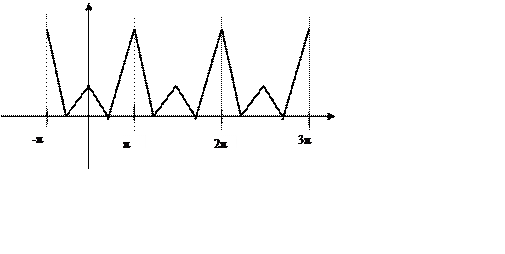
Исходную функцию  периодически продолжаем вне интервала  на всю ось, и функция, получившаяся в этом случае является периодической с периодом , и на интервале  она будет полностью совпадать с исходной функцией, следовательно, для нее можно применить разложение в ряд Фурье, рассмотренное ранее Если функция четная, то разложение [1], если нечетная – [2]..

2.  Случай половинного промежутка.

Допустим, произвольная функция  задана на промежутке . Для того, чтобы разложить эту  функцию в ряд Фурье, ее необходимо достроить ее произвольным способом на этом же промежутке. Существует 2 способа построения.

2.1.  построение симметрично оси ОУ.

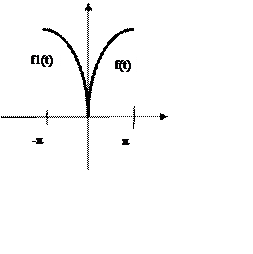
Получим .

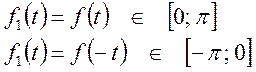
 будет четной на промежутке , тогда к этой функции можно применить разложение вида:

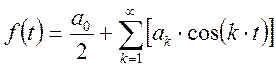
2.2.  построение симметрично оси ОХ.