Электротехника \ Электроэнергетические системы

Краткие теоретические сведения и методические советы по выполнению курсовой работы, страница 5

Для нашего примера действительные A(ω) и C(ω) и мнимая D(ω) части числителя и знаменателя коэффициента передачи (9) зависят от частоты и не только меняют свое значение, но и меняют знак. А это значит, что комплексные числа числителя и знаменателя меняют свое положение на комплексной плоскости. Это обстоятельство требует анализа аргументов числителя φчисл(ω) и знаменателя φзнам(ω) при изменении частоты от нуля до бесконечности.

1. Анализ числителя для определения его аргумента.

Действительная часть числителя равна A(ω)=1010–ω2. Если , т.е. , числитель представляет собой действительное и положительное число – A(ω) ≥ 0. Поэтому φчисл(ω)=0 при .

При , A(ω) < 0. Поэтому φ числ(ω)=.

2. Анализ знаменателя для определения его аргумента.

Действительная часть знаменателя равна действительной части числителя C(ω)=A(ω)=1010–ω2 и изменяется с изменением частоты также, как и числитель. Мнимая часть знаменателя D(ω)=0.3636·105ω прямо пропорциональна частоте ω и положительная D(ω)> 0 при ω > 0.

При  точка, отображающая знаменатель, находится в первом квадранте комплексной плоскости, причем при ω>0.8346 105 она пересекает биссектрису первого квадранта. Поэтому в диапазоне 0< ω<0.8346·105 при вычислении фазового угла знаменателя нужно использовать формулу 1 из таблицы 1: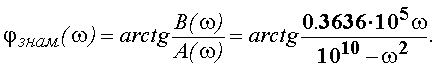 

При 0.8346·105 <ω 1.1982·105 отображающая точка находится в области 2 таблицы 1. Поэтому

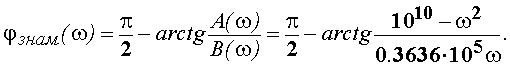
При ω >1.1982·105 точка переходит в область 4 таблицы 1.

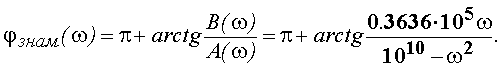
Таким образом, ФЧХ коэффициента передачи в нашем примере будет описываться различными формулами для четырех частотных областей.

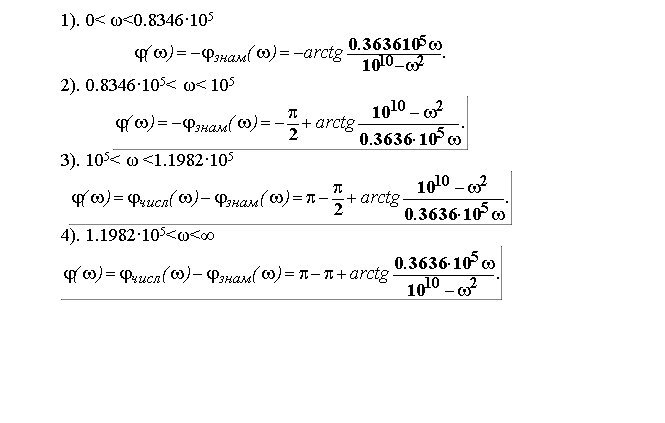Надпись: 1). 0< ω<0.8346·105 2). 0.8346·105< ω< 105 3). 105< ω <1.1982·105 4). 1.1982·105<ω<∞

1.6. Примеры расчёта частотных характеристик цепей

Пример 1.1. Для обобщенной одноконтурной цепи, представленной комплексной схемой замещения (рис.1.4) рассчитать ее частотные характеристики.

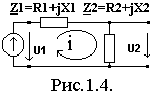1. Zвх(jw), Zвх(w), jz(w). 2. K(jw), K(w), jk(w).

Решение. 1) По определению Zвх(jw)=Ů1m/.Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:

Zвх(jw)=Ů1m/Ĭ1m= Ĭ1m(Z1+Z2)/ Ĭ1m =(R1+R2)+j(X1+X2)=R+jX;

Zвх(w)=[(R1+R2)²+(X1+X2)²]1/2;   jz(w)=arctg[(X1+X2)/(R1+R2)].

2) Используя определение К(jw) и законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ коэффициента передачи по напряжению:


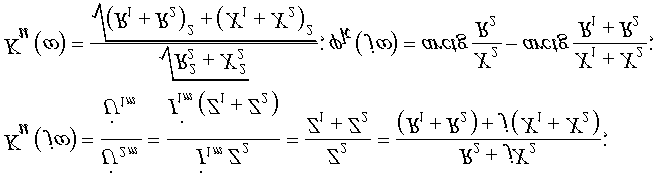Пример 1.2. Для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис.1.5), рассчитать ее частотные характеристики:

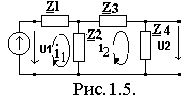1. Zвх(jw),  Zвх(w), jz(w).  2.K(jw), K(w), jk(w).

Решение. 1) Найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления.


По определению Zвх(jw)=Ů1m/.Входное сопротивление находим методом последовательных эквивалентных преобразований. Этот методсостоит в поэтапном преобразовании простых участков цепи. Они показаны на рис.1.6.

2. найдем КЧХ коэффициента передачи по напряжению. По определения Ku(jw)=Ů2m/Ů1m , а Ů2m=Z4Ĭ2 – находим по закону Ома.

Отсюда видно, что для расчета КЧХ необходимо найти Ĭ2. Находим Ĭ2 методом контурных токов. Для этого: определим число независимых контуров: Nk=в-у+1=3-2+1=2, каждому из них присвоим свой контурный ток I1, I2 и составим уравнения по методу контурных токов.

Z11Ĭ1+Z12Ĭ2=E11

Z21Ĭ1+Z22Ĭ2=E22 , где: Z11 – собственное сопротивление первого контура, Z11=Z1+Z2;

Z12 и Z21 сопротивление смежных контуров, Z12= Z21= - Z2 ;

Z22-собственное сопротивление II контура.           Z22=Z2+Z3+Z4 ;

E11-алгебраическая сумма источников ЭДС  I-ого контура, E11=U1m;

E22- алгебраическая сумма источников ЭДС II-ого контура, во II контуре источников ЭДС нет, E22=0. Найдем I2- ток второго контура (по методу Крамера), а затем и КЧХ коэффициента передачи по напряжению:


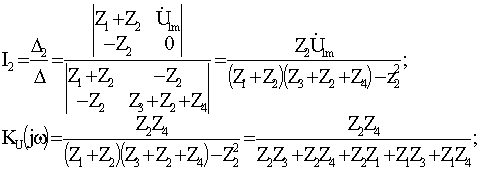Покажем другой способ нахождения КЧХ коэффициента передачи по напряжению. Найдем КЧХ, используя для расчета U2m  метод узловых потенциалов. Для этого:

Скачать файл