Краткие теоретические сведения и методические советы по выполнению курсовой работы, страница 4

Формула ФЧХ (уравнение ФЧХ) выражает зависимость аргумента (фазового угла) комплексной функции Кu(jω) от частоты:

φ(ω)=φ_числ(ω)–φ_знам(ω),                                           (7)

где φ _числ(ω) - аргумент числителя Н(jω), φ _знам(ω) - аргумент знаменателя Н(jω).

При записи формул для φ _числ(ω) и φ _знам(ω) следует учитывать, что фазовый угол произвольного комплексного числа Z=А(ω)+jВ(ω) вычисляется по различным формулам в зависимости от положения комплексного числа на комплексной плоскости (см. табл. 1.1).       

Таблица 1.1.

Отсюда следует, что уравнение ФЧХ может быть записано несколькими формулами, каждая из которых справедлива некотором своем диапазоне частот. Граничные частоты диапазонов можно оценить приближенно, так как в точках, близких к биссектрисам координатных квадрантов, можно пользоваться формулами обеих соседних областей.

Рассмотрим первый пример. Для схемы 3 приведенной в табл.3.2 частотная характеристика коэффициента передачи имеет вид:

К(jω)= {(jω)²R₁C₁R₂C₂}/{(1+(jω)²R₁C₁R₂C₂)+ jω(R₁C₁+R₂C₂+R₁C₂)}=

= {А(ω)}/{С(ω)+ jD(ω)}, где А(ω)=-(ω)²А₁; С(ω)= 1-(ω)²А₁; D(ω)= ωВ₁, А₁= R₁C₁R₂C₂, В₁=R₁C₁+R₂C₂+R₁C₂.

Формула ФЧХ вычисляется из выражения

φ(ω)=φ_числ(ω)–φ_знам(ω),

1.  Анализ числителя для определения его аргумента.

Действительная часть числителя при любой частоте А(ω)=-(ω)²А₁<0 - отрицательна, а мнимая часть отсутствует т.е. всегда равна нулю В(ω)=0. Следовательно, точка отображающая числитель всегда находится на отрицательной части реальной оси т. е.

φ_числ(ω)=π.

2.  Анализ числителя для определения его аргумента.

Мнимая часть знаменателя при любой частоте положительна, а действительная знакопеременная, следовательно точка отображающая знаменатель находится в первом или втором квадранте комплексной плоскости и для вычисления аргумента знаменателя нужно использовать формулу 2 из таблицы1.1.

φ_знам(ω)= π/2 - arctg( (1-ω² А₁)/ ω В₁ ).

Таким образом окончательно, ФЧХ коэффициента передачи для нашего примера имеет вид

φ(ω)= π- (π/2 - arctg( (1-ω²А₁)/ ωВ₁))= π/2 + arctg( (1-ω²А₁)/ ωВ₁)).

Рассмотрим второй, более сложный, пример. Частотная характеристика цепи задана выражением

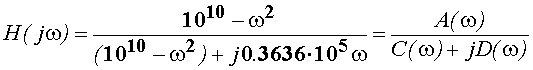.                 (9)

где A(ω)=(10¹⁰–ω ²) ,      B(ω)=0,  C(ω)=(10¹⁰ –ω ²),           D(ω)=0.3636·10⁵ω.

Учитывая (8), получим выражение  для АЧХ

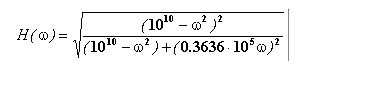
(10)

Формула ФЧХ выражает зависимость аргумента (фазового угла) комплексной функции K_U(jω) от частоты и имеет вид:

(11)

где     φ _числ(ω) – аргумент комплексного числителя H(jω),

φ _знам(ω) – аргумент комплексного знаменателя H(jω).

При записи формул для φ _числ(ω) и φ _знам(ω) следует учитывать, что фазовый угол произвольного комплексного числа Z(jω)=А(ω)+jB(ω) вычисляется различным образом в зависимости от положения комплексного числа на комплексной плоскости (см. таблицу 1.1).

Отсюда следует, что выражение ФЧХ может быть записано несколькими формулами, каждая из которых справедлива в некотором своем диапазоне частот. Граничные частоты диапазонов можно оценить приближенно, так как в точках, близких к биссектрисам координатных квадрантов, можно пользоваться формулами обеих соседних областей.