Определение. Задача нахождения решения уравнения
![]() , удовлетворяющего
условию
, удовлетворяющего
условию
![]() (5.10)
(5.10)
называется задачей Коши.
Условие (5.10) называется начальным условием.
Теорема Коши (о
существовании и единственности решения задачи Коши). Пусть ![]() непрерывна в некоторой
окрестности точки
непрерывна в некоторой
окрестности точки ![]() и имеет в этой окрестности
ограниченную частную производную
и имеет в этой окрестности
ограниченную частную производную ![]() , т.е.
, т.е. ![]() . Тогда в некотором интервале
. Тогда в некотором интервале ![]() существует единственное решение задачи
Коши
существует единственное решение задачи
Коши
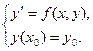
Геометрический смысл теоремы Коши заключается в том, что через каждую точку, удовлетворяющую условиям теоремы Коши, проходит только одна интегральная кривая.
Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
![]() . (5.11)
. (5.11)
Способ решения. Считая, что ![]() , разделим
обе части уравнения (5.11) на
, разделим
обе части уравнения (5.11) на ![]() и умножим на
и умножим на ![]() :
: ![]() . Проинтегрировав обе части, получим:
. Проинтегрировав обе части, получим:
![]() .
.
Пример. ![]() .
. ![]() ;
; ![]() ;
; ![]() .
.
Замечание. Уравнения с разделяющимися переменными может иметь и другой вид. Например,
![]()
Определение. Функция ![]() называется однородной
степени
называется однородной
степени ![]() функцией, если для всех
функцией, если для всех ![]() выполняется равенство
выполняется равенство
![]() .
.
Определение. Дифференциальное уравнение
![]() (5.12)
(5.12)
называется однородным,
если ![]() однородная функция степени 0, то есть
если
однородная функция степени 0, то есть
если
![]() .
.
Способ решения. Сделаем в уравнении (5.12) замену ![]() :
:
![]() .
.
Так как ![]() однородная функция степени 0, то
однородная функция степени 0, то ![]() и получаем уравнение
и получаем уравнение ![]() , которое является уравнением с
разделяющимися переменными. Разделим переменные:
, которое является уравнением с
разделяющимися переменными. Разделим переменные: ![]() .
Проинтегрировав обе части, подставляем вместо
.
Проинтегрировав обе части, подставляем вместо ![]() выражение
выражение
![]() .
.
Рассмотрим уравнение вида
![]() (5.13)
(5.13)
Это уравнение можно привести к виду
![]() .
.
Если ![]() -
однородная функция степени
-
однородная функция степени ![]() , а
, а ![]() - однородная функция степени
- однородная функция степени ![]() , то
, то
![]() .
.
Определение. Уравнение вида
![]() (5.14)
(5.14)
называется линейным.
Если ![]() , то
уравнение называется однородным линейным. Если
, то
уравнение называется однородным линейным. Если ![]() , то уравнение называют неоднородными
линейным.
, то уравнение называют неоднородными
линейным.
Линейные дифференциальные уравнения можно решать с помощью метода Лагранжа или метода Бернулли.
Метод вариации произвольных постоянных (метод Лагранжа)
Сначала находим решение однородного уравнения, соответствующего уравнению (5.14):
![]() .
.
![]()
![]() .
.
Затем ищем решение неоднородного уравнения (5.14) в виде
![]() . (5.15)
. (5.15)
Подставляем (5.15) в уравнение (5.14):
![]() ,
,
![]() .
.
Отсюда
находим ![]() . Подставляя
. Подставляя ![]() в
(5.15), получаем решение уравнения (5.14):
в
(5.15), получаем решение уравнения (5.14):
![]() .
.
Пример. Решить уравнение ![]() . Воспользуемся
методом Лагранжа.
. Воспользуемся
методом Лагранжа.
1) Найдем решение однородного уравнения
![]() .
.
![]()
Будем искать решение неоднородного уравнения в виде
![]() . (5.16)
. (5.16)
Подставим (5.16) в
исходное уравнение: ![]() . Упрощая, получаем:
. Упрощая, получаем: ![]() . Находим отсюда функцию
. Находим отсюда функцию ![]() :
:
![]() .
.
2) Подставляя полученное выражение в (5.16), получаем решение исходного уравнения:
![]() .
.
Определение. Уравнением Бернулли называется уравнение вида
![]() (5.17)
(5.17)
Уравнение Бернулли решается методом Бернулли, который заключается в следующем.
Решение уравнения (5.17) ищется в виде
![]() . (5.18)
. (5.18)
Подставим (5.18) в уравнение (5.17):
![]() .
.
В левой части вынесем
за скобки, например, функцию ![]() :
:
![]() (5.19)
(5.19)
Функцию ![]() выбираем так, чтобы выражение в
скобках равнялось нулю:
выбираем так, чтобы выражение в
скобках равнялось нулю:
![]() . (5.20)
. (5.20)
![]() .
.
Так как нас устраивает
любая функция ![]() , удовлетворяющая уравнению
, удовлетворяющая уравнению
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.