8.1. Кривизна графика функции
8.2. Вершины кривых
8.3. Радиус кривизны
8.4. Упражнения
10. Векторная алгебра
10.1. Определение вектора
10.2. Операции над векторами
10.3. Разложение вектора по базису
10.4. Линейная зависимость векторов
10.5. Система координат и координаты вектора
10.6. Проекции вектора
10.7. Скалярное произведение
10.8. Векторное произведение
10.9. Выражение векторного произведения через координаты сомножителей
10.10. Смешанное произведение
10.11. Нахождение координат вектора в произвольном базисе
11. Прямые линии и плоскости
11.1. Уравнение поверхности
11.2. Уравнение плоскости
11.3. Изображение плоскости
11.4. Угол между плоскостями
11.5. Расстояние от точки до плоскости
11.6. Прямая на плоскости
11.7. Прямая в пространстве
11.8. Основные задачи на прямую и плоскость
12. Кривые второго порядка
12.1. Окружность
12.2. Эллипс
12.3. Гипербола
12.4. Парабола
12.5. Параллельный перенос системы координат
13. Поверхности второго порядка
13.1. Сфера
13.2. Эллипсоид
13.3. Гиперболоиды
13.4 Конус
13.5 Параболоиды
13.6 Цилиндры
13.7 Параллельный перенос системы координат
8.1. Кривизна графика функции
Определение 8.1.
Пусть кривая L задана как график функции y = f (x)
и M0(x0;f (x0)) —
некоторая точка этой кривой. Будем предполагать, что функция f (x)
дифференцируема в некоторой окрестности точки x0, так что при
x из этой окрестности к графику y = f (x) можно
проводить касательные, составляющие угол ![]() (x)
с осью Ox. Кривизной кривой L в точке M0
(или при x = x0) называется число
(x)
с осью Ox. Кривизной кривой L в точке M0
(или при x = x0) называется число
k(x0) = ![]()
![]()
![]()
![]() , где
, где ![]()
![]() =
= ![]() (x)
-
(x)
- ![]() (x0)
— угол поворота касательной при переходе точки касания из M0(x0;f
(x0)) в M(x;f (x)) и
(x0)
— угол поворота касательной при переходе точки касания из M0(x0;f
(x0)) в M(x;f (x)) и ![]() l —
длина части линии21
L между точками M0 и M.
l —
длина части линии21
L между точками M0 и M.
Смысл предела, определяющего кривизну, — это скорость поворота касательной в точке M0, в расчёте на единицу длины дуги.

Рис.8.1. Поворот касательной при переходе из точки M0 в точку M
Теоpема Пусть в точке x0 функция f (x) имеет вторую производную f''(x0). Тогда кривизна линии L = {y = f (x)} при x = x0 равна
k(x0) = ![]() .
.
Доказательство
Пусть x = x0 + h — точка, близкая к x0
(будем считать для наглядности, что h > 0). По геометрическому смыслу
производной, tg ![]() (x)
= f'(x), откуда
(x)
= f'(x), откуда ![]() (x)
= arctg f'(x). При малых h дуга M0M
весьма близка к хорде M0M, и интуитивно ясно, что для
гладкой кривой L предел отношения длины дуги
(x)
= arctg f'(x). При малых h дуга M0M
весьма близка к хорде M0M, и интуитивно ясно, что для
гладкой кривой L предел отношения длины дуги ![]() l
к длине хорды | M0M| равен 1, то есть эти две
бесконечно малых при h
l
к длине хорды | M0M| равен 1, то есть эти две
бесконечно малых при h![]() 0 величины
эквивалентны22.
Хорда имеет длину | M0M| =
0 величины
эквивалентны22.
Хорда имеет длину | M0M| = ![]() ,
где
,
где ![]() x = h
и
x = h
и ![]() y = f
(x) - f (x0) — приращения координат при
переходе от точки M0 к точке M. Рассмотрим предел
y = f
(x) - f (x0) — приращения координат при
переходе от точки M0 к точке M. Рассмотрим предел ![]()
![]() . Имеем,
очевидно,
. Имеем,
очевидно,
![]() =
= ![]() =
= ![]() , откуда
, откуда
![]()
![]() =
= ![]() .
.
Поскольку ![]() l
l ![]() | M0M|,
то, заменив числитель на эквивалентную бесконечно малую, получаем, что
| M0M|,
то, заменив числитель на эквивалентную бесконечно малую, получаем, что
![]()
![]() =
= ![]() .
.
Теперь преобразуем отношение ![]() к
виду
к
виду ![]() . Имеем
тогда
. Имеем
тогда
k(x0) = ![]()
![]()
![]()
![]() =
= ![]()
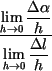
![]() =
= ![]()
![]()
![]() .
.
Осталось вычислить производную, стоящую в числителе:
![]()
![]() (x) = (arctg f'(x))' =
(x) = (arctg f'(x))' = ![]() .
.
Это приводит нас к доказываемой формуле
k(x0) = ![]()
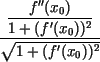
![]() =
= ![]() .
.
Пример 8.1.
Найдём кривизну параболы y = x2 при произвольном значении x. Поскольку y' = 2x и y'' = 2, имеем
k(x) = ![]() .
.
Заметим, что кривизна параболы убывает при росте | x| и принимает максимальное значение 2 при x = 0, то есть в вершине параболы.
8.2. Вершины кривых
По аналогии с параболой мы можем дать такое определение:
Определение 8.2.
Назовём вершиной кривой y = f (x) любую точку этой кривой, в которой кривизна k(x) имеет локальный экстремум.
В соответствии с этим определением вершина параболы y = x2 является вершиной линии y = x2 в новом, обобщённом, смысле.
Пример 8.2.
Рассмотрим окружность x2 + y2 = R2.
Её верхняя половина (при y ![]() 0) — это
график функции y =
0) — это
график функции y = ![]() на отрезке
[- R;R]. Возьмём точку x
на отрезке
[- R;R]. Возьмём точку x ![]() (-R;R)
и найдём кривизну окружности при этом x. Имеем:
(-R;R)
и найдём кривизну окружности при этом x. Имеем:
y' = - ![]() ,
,
y'' = - ![]() , откуда
, откуда
k(x) = 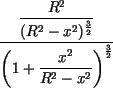 =
= ![]() =
= ![]() .
.
Получаем, что кривизна окружности в любой её точке одинакова и обратна радиусу окружности23.
Пример 8.3.
Рассмотрим прямую y = kx + b. Поскольку y'' = 0, то кривизна прямой в любой точке равна 0. Как и у окружности, все точки прямой — это её вершины.
Заметим, что, по определению, кривизна неотрицательна, так что если она
равна 0 в некоторой точке кривой y = f (x), то эта точка
является вершиной кривой. Поскольку k(x) = ![]() , это может
случиться лишь при f''(x) = 0, в частности, во всех точках перегиба
функции f (x) (тех, где вторая производная существует).
, это может
случиться лишь при f''(x) = 0, в частности, во всех точках перегиба
функции f (x) (тех, где вторая производная существует).
Пример 8.4.
Рассмотрим параболу четвёртой степени y = x4. Поскольку вторая производная y'' = 12x2 обращается в 0 при x = 0, то точка O(0;0) служит одной из вершин этой параболы: в ней кривизна принимает минимальное значение 0.
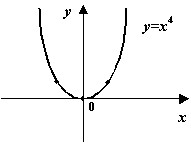
Рис.8.2. Парабола y = x4 имеет три вершины
Упражнение 8.1.
Найдите оставшиеся две вершины параболы четвёртой степени, в которых кривизна принимает максимальное значение.
Ответ: эти две вершины расположены при x
= ±![]() .
.
Пример 8.5.
Рассмотрим гиперболу y = ![]() (a
> 0). Поскольку y' = -
(a
> 0). Поскольку y' = - ![]() и y''
=
и y''
= ![]() , имеем
, имеем
k(x) = ![]()
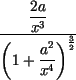
![]() =
= ![]() .
.
Пример 8.6.
Найдём точку локального максимума кривизны гиперболы и покажем, что вершина гиперболы как кривой совпадает с её вершиной, понимаемой как пересечение гиперболы с её осью симметрии y = x.
Рассмотрим часть гиперболы, лежащую при x > 0 (вторая половина
— симметрична рассматриваемой). Поскольку z = t![]() —
возрастающая при t
—
возрастающая при t ![]() 0 функция,
точки экстремума функций k(x) и
0 функция,
точки экстремума функций k(x) и
f (x) =
(k(x))![]() = (2a)
= (2a)![]()
![]() совпадают. Ввиду того, что функция t = x2
также возрастает при x
совпадают. Ввиду того, что функция t = x2
также возрастает при x ![]() 0,
достаточно сделать замену x2 = t и перейти к
нахождению экстремума функции
0,
достаточно сделать замену x2 = t и перейти к
нахождению экстремума функции
g(t) = ![]() , график которой при t
, график которой при t ![]() 0
имеет такой вид:
0
имеет такой вид:
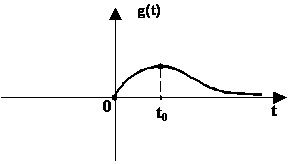
Рис.8.3. График
функции g(t) = ![]()
Точка максимума t0 ищется из условия g'(t0) = 0; легко подсчитать
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.