37. Критерий независимости СВ.
Пусть Х, У - двум. с - ма непрер. СВ.
Условной вероятностью распр - я сост - я сост. Х при данном Y=у F(х/у) наз. отнош. плотн. (совм. распред. F(х,у) ) с - мы к плотности с - мы F2(Y)
![]()
f(x,y) отличная от f(x)
f(x) дает независ. от значения которые приним. состовл. , хар-ку.
f(x,y) дает от значения которые приним. состовл. , хар-ку.
![]()
Св-ва условной плотности распределения.
![]()
![]()
Две СВ независимы , если закон распр. состоящий из них не зависит от таго , какие значения принимает другая величина.
Теорема: Для того, чтобы СВ X и Y были независимы необходимо и достаточно , чтобы ф - ция распределения системы СВ F(х,у) была =произведению ф - ции распр. состовляющих
![]()
Докозательство:
1. Необходимость: Пусть Х и Y независемы, тогда независимы и события
X<x Y<y
Тогда вероятность того , что X<x , Y<y двух независемых событий это вероятностей P(Х<x) и P(Y<y)
![]()
2. Достаточность:
Нужно докозать что X и Y - независимы при условии:
![]()
![]() => эти события независимы значит
события X<x , Y<y - независимы следовательно и сами СВ X
и Y независимы ч.т.д.
=> эти события независимы значит
события X<x , Y<y - независимы следовательно и сами СВ X
и Y независимы ч.т.д.
Следствие:
Для того, чтобы непр. СВ были независимы необходимо и достаточно, чтобы плотность совместного распределения системы (х,у) была = произведению состовляющих.
38. Кореляционный момент Мху и коэффициент кореляции двух СВ.
Кореляционным моментом системы двух СВ (![]() ) называют мат. ожидание произв.
отклон. этих СВ от их мат.ожид.
) называют мат. ожидание произв.
отклон. этих СВ от их мат.ожид.
![]()
Для вычисления коор. момента дискретной СВ используется формулу:
![]()
Для непрерывной СВ:
![]()
![]()
Д-ть, что корреляционный момент двумерной СВ=![]()
Коор. момент служит для характеристики связи М/у СВ X и Y (т.е. зависит или не зависит ).
Теорема: Коор момент двух независимых СВ = 0.
Доказательство:
X,Y - независимы , x - М(х) и у - М(у) независимы
![]() т.к. М(x - М(х)) = 0
т.к. М(x - М(х)) = 0
ч.т.д.
Недостаток:
Корр. момент зависит от единиц измерения. Если
СВ см , то ![]() если в м , то
если в м , то ![]() .
.
Чтобы исправить этот недостаток, ввод. коэф.
корреляции ![]() - это отношение корр. момента к
произведению сред. отношений.
- это отношение корр. момента к
произведению сред. отношений.
![]()
Св-ва коррел. хар-к:
1. Теорема: Абс. величина коор момента двух СВ X и Y не превышает среднего геометрического их дисперсий
![]()
Доказательство:
Рассмотрим СВ ![]() и найдем ее дисперсию
и найдем ее дисперсию
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ч.т.д.
2. Теорема:
Абс. вел. коэф. коррел.![]() (
(![]() )
)
Док-во: ![]()
![]()
39. Коррелированность и зависимость СВ.
Две СВ называются коррел. , если их коррел.момент , а следов-но и коэффициент корреляции отличен от нуля.
Две СВ называются не коррел. если ![]() .
.
Кореляционным моментом системы двух СВ называют мат. ожидание произв. отклон. этих СВ от их мат. ожид.
![]()
Для вычисления коор. момента дискретной СВ используется формулу:
![]()
Для непрерывной СВ:
![]()
![]()
Из зависимости двух СВ не следует их коррел.
Пример: пусть двумер. СВ X ,Y задана своей пл-тю распр-я (внутри эллипса)
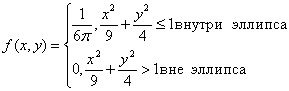
Док-ть, что СВ x,y завис. и некоррел. велич. Зависимы, если их ф-ции распр. с-мы = произв-ю их ф-й распр-я .
Независимы, если плотн. с-мы = x плотности.
Завис. ![]()

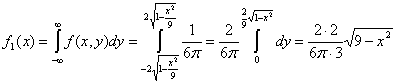
из Ур-я ![]()
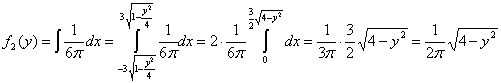
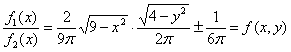 ,
,
![]() пл-ти распр.
вер-ей, знач. завис. велич.
пл-ти распр.
вер-ей, знач. завис. велич.
Некоррелир.: найти коэф. корреляции
![]()
![]()
Мат. ожид. =0 для этих СВ, т.к. они симметричны относительно OX и относ. OY.
![]() , знач.
некоррел., т.к. =0
, знач.
некоррел., т.к. =0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.