Кафедра медицинской и биологической физики
Тема: Основы математической статистики. Проверка статистических гипотез
лекция № 3 для студентов 1 курса, обучающихся по специальности 060101 – Лечебное дело К.п.н., доцент Красноярск, 2013
План лекции:
Нормальный закон распределения случайных величин
Нормальное распределение возникает тогда, когда на изменение случайной величины действует множество различных независимых факторов, каждый из которых в отдельности не имеет преобладающего значения.
ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ:
ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ:
![]()
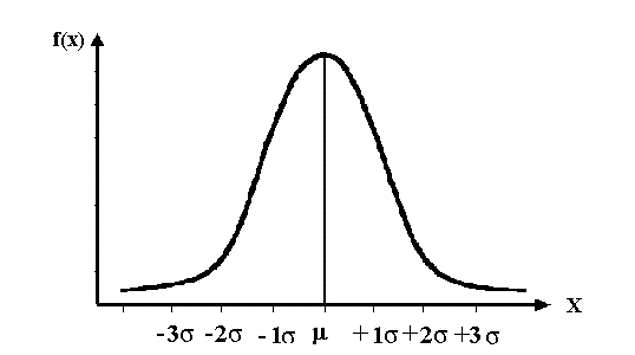
Рис.1. Кривая нормального распределения
Функция нормального закона
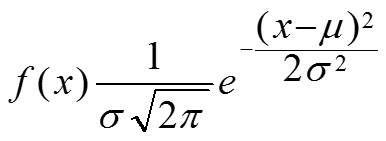
функция плотности распределения вероятностей
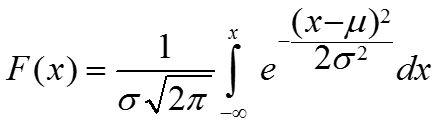
функция распределения вероятностей
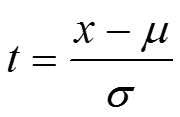
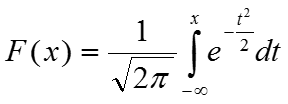
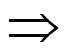
Вероятность попадания значения случайной величины в интервал от а до b:
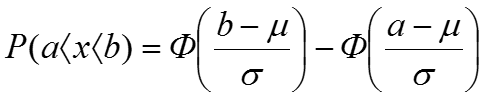
причем Ф(–t) = 1– Ф(t)
КОЭФФИЦИЕНТ АСИММЕТРИИ
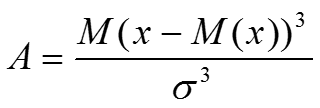
А>0 - правоасимметричные, А<0 - левоасимметричные
f(x)
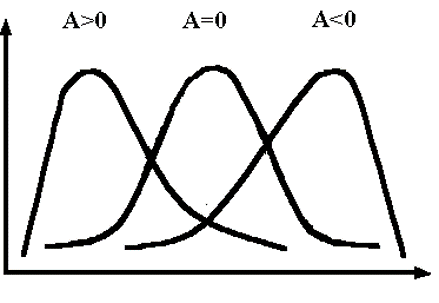
X
ПОКАЗАТЕЛЬ ЭКСЦЕССА
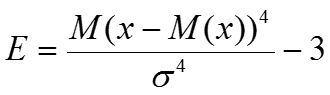
f(x)
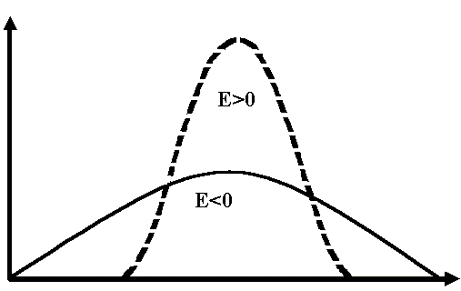
Х
Точечные оценки случайной величины:
Математическое ожидание дискретной случайной величины
(среднее значение) равно сумме произведений значений, принимаемых этой величиной, на соответствующие им вероятности:
Дисперсия дискретной случайной величины это математическое ожидание квадрата соответствующего отклонения случайной величины x от ее математического ожидания:

Основные числовые характеристики непрерывных случайных величин

Математическое ожидание

Дисперсия
Среднее квадратическое отклонение для дискретной и непрерывной случайной величины

Интервальные оценки
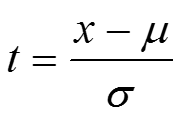
нормированное отклонение х – μ=σt
![]()
1σ – 68,3%;
2σ – 95,5%;
![]()
![]()
3σ – 99,7% всех вариант
Доверительные вероятности и доверительные интервалы
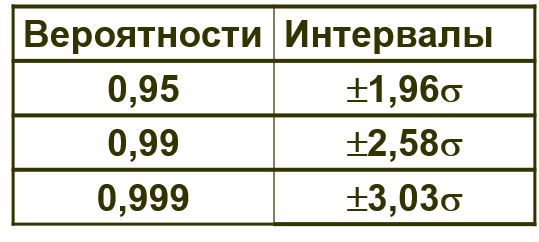
=1 – Р уровень значимости
Генеральная и выборочные совокупности
Сравнительная характеристика
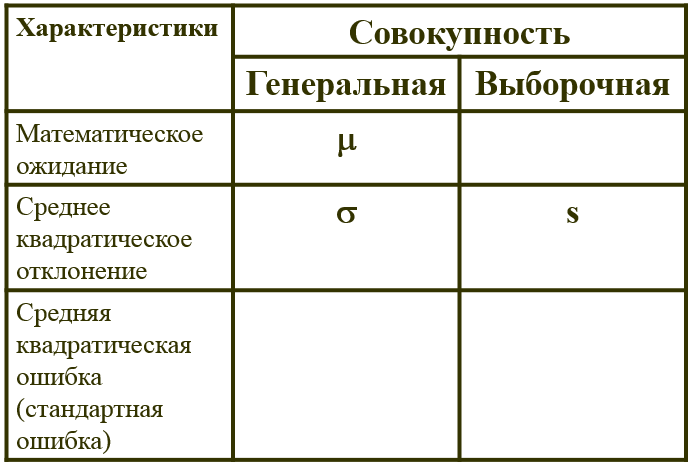
![]()
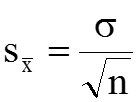
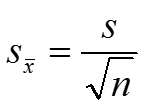
значение генеральной средней с доверительным интервалом
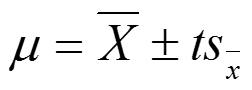
Сравнение теоретических и эмпирических распределений
Средние квадратические ошибки sА (асимметрии) и sЕ (эксцесса)
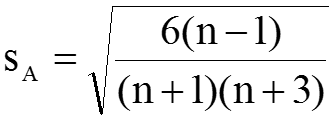
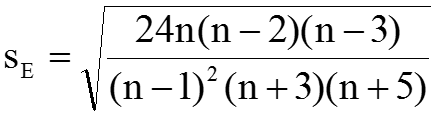
Для достаточно большой выборки (n>30), если показатели асимметрии (А) и эксцесса (Е) в два и более раза превышают показатели их средних квадратических ошибок, гипотезу о нормальности распределения нужно отвергнуть.
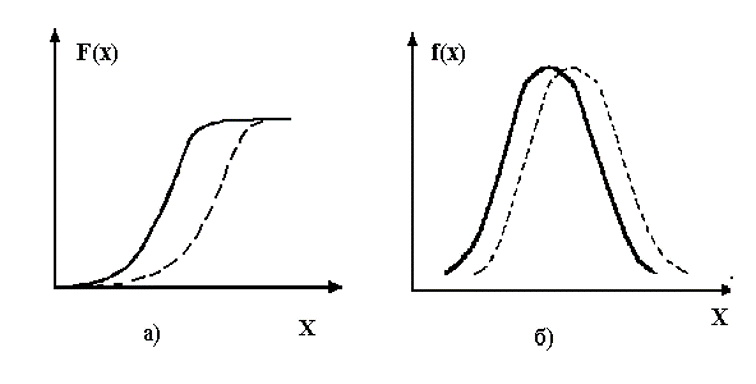
Сравнение теоретических и экспериментальных распределений по: а) критерию Колмогорова – Смирнова, б) критерию Пирсона. Пунктирная линия – эмпирическое распределение, сплошная – теоретическое распределение.
Критерий Пирсона
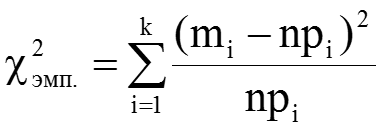
где mi – экспериментальные частоты попадания значения случайной величины в интервал, npi – теоретические частоты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.