Няхай зададзена лікавае мноства
![]() , і кожнаму
, і кожнаму
![]() паводле
некаторага правіла
паводле
некаторага правіла ![]() ставіцца
ў адпаведнасць адзін лік
ставіцца
ў адпаведнасць адзін лік ![]() .
Тады гавораць, што на мностве
.
Тады гавораць, што на мностве ![]() вызначана
лікавая функцыя (або проста функцыя) і пішуць
вызначана
лікавая функцыя (або проста функцыя) і пішуць ![]() .
.
Зменную х называюць незалежнай
зменнай або аргументам функцыі, мноства ![]() – абсягам
вызначэння функцыі
– абсягам
вызначэння функцыі ![]() .
Для абазначэння абсягу вызначэння і мноства значэнняў функцыі
.
Для абазначэння абсягу вызначэння і мноства значэнняў функцыі ![]() карыстаюцца
адпаведна сімваламі
карыстаюцца
адпаведна сімваламі ![]() і
і ![]() .
.
Калі кожнаму натуральнаму ліку (нумару) ![]() ставіцца ў
адпаведнасць лік
ставіцца ў
адпаведнасць лік ![]() , то
гавораць, што зададзена лікавая паслядоўнасць
, то
гавораць, што зададзена лікавая паслядоўнасць ![]() або, карацей, паслядоўнасць
або, карацей, паслядоўнасць
![]() . Інакш кажучы,
паслядоўнасцю называюць функцыю, зададзеную на мностве натуральных лікаў. Лік
. Інакш кажучы,
паслядоўнасцю называюць функцыю, зададзеную на мностве натуральных лікаў. Лік ![]() называюць n-ым элементам
паслядоўнасці. Паслядоўнасць можа быць зададзена формулай агульнага элемента
называюць n-ым элементам
паслядоўнасці. Паслядоўнасць можа быць зададзена формулай агульнага элемента ![]() ; рэкурэнтнай
формулай, напрыклад
; рэкурэнтнай
формулай, напрыклад ![]() ;
іншымі спосабамі.
;
іншымі спосабамі.
2.1.
Няхай зададзена
функцыя ![]() . Знайдзіце
. Знайдзіце ![]()
![]() і дакажыце,
што гэтыя лікі ўтвараюць арыфметычную прагрэ-сію.
і дакажыце,
што гэтыя лікі ўтвараюць арыфметычную прагрэ-сію.
2.2.
Знайдзіце f(0), f(x) + 2, f(x+ 2), f(![]() ),
1/f(x), калі:
1) f(x) =
),
1/f(x), калі:
1) f(x) = ![]() ; 2) f(x) = x
; 2) f(x) = x![]() – 2x+ 2.
– 2x+ 2.
2.3.
Знайдзіце f(x), калі: 1) f(x+ 1)=2 x+ 3; 2) f(![]() ) =
) = ![]() .
.
2.4.
Зададзена функцыя Дырыхле
D(x) = 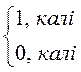
![]()
![]()
![]() 1) Знайдзіце
D(3/4), D(
1) Знайдзіце
D(3/4), D(![]() ), D(log
), D(log![]() 8).
2) Дакажыце, што D(x+
8).
2) Дакажыце, што D(x+ ![]() ) = D(x) для любых цэлых p і q.
) = D(x) для любых цэлых p і q.
2.5.
Функцыя sgn x (чытаецца сігнум ікс) задаецца
формулай
sgn x=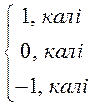
![]() . 1) Дакажыце, што xsgn x=
. 1) Дакажыце, што xsgn x= ![]() .
2) Знайдзіце sgn x
пры x= sin
.
2) Знайдзіце sgn x
пры x= sin![]() , x= sin
, x= sin![]() , x= sin
, x= sin![]()
![]() .
.
2.6.
Зададзена функцыя
Хэвісайда η(x)=![]()
![]()
![]() Знайдзіце:
1) η(х – а); 2) η(х – а)+η(х –
b).
Знайдзіце:
1) η(х – а); 2) η(х – а)+η(х –
b).
2.7.
Няхай зададзены чатыры
лікі х![]() , х
, х![]() , y
, y![]() , y
, y![]() , прычым
, прычым ![]() . Праверце, што
функцыя P(x)=
. Праверце, што
функцыя P(x)=![]() з’яўляецца мнага-складам не вышэй чым першай
ступені і задавальняе ўмовы
P(x
з’яўляецца мнага-складам не вышэй чым першай
ступені і задавальняе ўмовы
P(x![]() ) = y
) = y![]() , P(x
, P(x![]() ) = y
) = y![]() .
.
2.8.
Няхай зададзены тры
розныя лікі х![]() , х
, х![]() , х
, х![]() і любыя лікі у
і любыя лікі у![]() , у
, у![]() , у
, у![]() . Праверце, што
функцыя
P(x)=
. Праверце, што
функцыя
P(x)=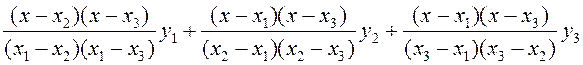 з’яўляецца мнагаскладам не вышэй, чым другой ступені, прычым P(x
з’яўляецца мнагаскладам не вышэй, чым другой ступені, прычым P(x![]() ) = y
) = y![]() , P(x
, P(x![]() ) = y
) = y![]() , P(x
, P(x![]() ) = y
) = y![]() .
.
2.9.
Знайдзіце мнагасклад Р(х)
ступені не вышэй за n, які задавальняе ўмовы P(x![]() ) = y
) = y![]() , P(x
, P(x![]() ) = y
) = y![]() , …, P(x
, …, P(x![]() ) = y
) = y![]() , дзе х
, дзе х![]() , у
, у![]() ,
, ![]() – любыя
зададзеныя лікі, прычым x
– любыя
зададзеныя лікі, прычым x![]()
![]() x
x![]() , калі i
, калі i![]() j. ( Р(х) у такім выпадку
называюць інтэрпаляцыйным мнагаскладам.)
j. ( Р(х) у такім выпадку
называюць інтэрпаляцыйным мнагаскладам.)
2.10.
Дакажыце, што функцыя f(x)=![]() задавальняе ўмовы:
1)
задавальняе ўмовы:
1) ![]() = – f(x); 2) x
= – f(x); 2) x![]() = 1.
= 1.
2.11.
Знайдзіце абсяг
вызначэння наступных функцый:
1) f(x) = ![]() ; 2) f(x) =
; 2) f(x) = ![]()
![]() ; 3) f(x) =
; 3) f(x) = ![]() ;
4) f(x) =
;
4) f(x) = ![]() (a
(a![]() ); 5) f(x) =
); 5) f(x) = ![]() ; 6) f(x) =
; 6) f(x) = ![]() ; 7) f(x) = lg(
; 7) f(x) = lg(![]() ); 8) f(x) = arcsin(1–х); 9) f(x) =
); 8) f(x) = arcsin(1–х); 9) f(x) = ![]() .
.
2.12.
Прывядзіце прыклад
функцый f(x) і g(x), зададзеных формуламі, у якіх: 1) D(f) = ![]() за выключэннем пунктаў х = 0, х =
1, х =2;
2)D(g) =
за выключэннем пунктаў х = 0, х =
1, х =2;
2)D(g) = ![]() [c; d], дзе a<b<c.
[c; d], дзе a<b<c.
2.13.
Знайдзіце мноства
значэнняў функцыі:
1) f(x) = 2x–4, x![]() [–2, 2]; 2) f(x) =
[–2, 2]; 2) f(x) = ![]() , x
, x![]() [0, 3]; 3)
[0, 3]; 3) ![]() = 2x+ sgnx, x
= 2x+ sgnx, x![]()
![]() ;
4)
;
4) ![]() = x
= x![]() , x
, x![]() [–2, 1]; 5) f(x) = x+
[–2, 1]; 5) f(x) = x+![]() , x
, x![]() (0, +
(0, +![]() ).
).
2.14.
Знайдзіце φ(f(x)) і f(φ(x)) , ці кампазіцыі φ![]() f і f
f і f![]() φ, калі:
1) φ(x) = x
φ, калі:
1) φ(x) = x![]() , f(x) = 10
, f(x) = 10![]() ; 2) φ(x) =
; 2) φ(x) = ![]()
![]()
![]() f(x) = 2x
f(x) = 2x![]() + 1.
+ 1.
2.15.
Няхай ![]() ,
, ![]() ,
, ![]() . Запішыце
формулы, якія задаюць кампазіцыі: 1) f
. Запішыце
формулы, якія задаюць кампазіцыі: 1) f![]() g
g![]() φ; 2) g
φ; 2) g![]() φ
φ![]() f ; 3) φ
f ; 3) φ![]() g
g![]() f .
f .
2.16. Няхай ![]() (n-кампазіцый). Знайдзіце f
(n-кампазіцый). Знайдзіце f![]() (x), f
(x), f![]() (x) і f
(x) і f![]() (x) калі: 1)f(x) =
(x) калі: 1)f(x) = ![]() ; 2) f(x) = 2x+ 1; 3) f(x) = ax+ b.
; 2) f(x) = 2x+ 1; 3) f(x) = ax+ b.
2.17. Зададзена функцыя f(x). Ці заўсёды існуюць дзве такія функцыі φ(x) і g(x) (φ(x)![]() x, g(x)
x, g(x)![]() x), што f(x) = φ(g(x)) ?
x), што f(x) = φ(g(x)) ?
2.18.
Знайдзіце абсяг
вызначэння складанай функцыі f(g(x)), калі:
1) f(x) = lg x![]() , g(x) = sin x;
2) f(x) = sin x, g(x) = lg x
, g(x) = sin x;
2) f(x) = sin x, g(x) = lg x![]() .
.
2.19. Пабудуйце графікі функцый:
1) y=
x+ 2;
2) y= ![]() ;
3) y= 2x– 3x
;
3) y= 2x– 3x![]() ;
4) y=
;
4) y=![]() ; 5) y=
; 5) y= ![]() ;
6) y=
;
6) y= ![]() ;
7) y= x+
;
7) y= x+ ![]() ;
8) y= sinax, а = 1; 2;
;
8) y= sinax, а = 1; 2; ![]() ,
0
,
0 ![]() x
x![]() 2
2![]() ;
9)y=sgn(x
;
9)y=sgn(x![]() –4);
10) y= sgn(sinx);
11) y=
–4);
10) y= sgn(sinx);
11) y= ![]() , дзе
, дзе ![]() –
цэлая частка x;
12) y=
–
цэлая частка x;
12) y= ![]() , дзе
, дзе ![]() – дробная
частка x;
13) y= cosx+
– дробная
частка x;
13) y= cosx+ ![]() .
.
2.20.
У адной сістэме
каардынат пабудуйце графікі функцый ![]() ,
калі: 1) p= 1, 2, 3; 3) p= –1, –2, –3;
2) p= 1,
,
калі: 1) p= 1, 2, 3; 3) p= –1, –2, –3;
2) p= 1, ![]() ,
,![]() ; 4) p= –1,
; 4) p= –1, ![]() ,
, ![]() .
.
2.21.
Пабудуйце графікі
функцый ![]() ,
, ![]() , –
, –![]() ,
, ![]() ,
, ![]() ,
, ![]() , калі:
1)
, калі:
1) ![]() =
2x– 1; 2)
=
2x– 1; 2) ![]() =
x– 2x
=
x– 2x![]() ; 3)
; 3) ![]() = cos 2x .
= cos 2x .
2.22. Чым адрозніваюцца графікі функцый ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (a> 0) ад графіка функцыі
, (a> 0) ад графіка функцыі ![]() ?
?
2.23. Знайдзіце 5 першых элементаў паслядоўнасці, зададзенай формулай агульнага
элемента:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]()
![]() ; 4)
; 4) 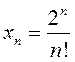 ; 5)
; 5) ![]() ; 6)
; 6) 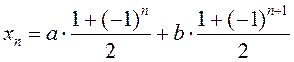 ; 7)
; 7) 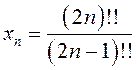 , дзе
, дзе ![]() ,
, ![]() .
.
2.24.
Паслядоўнасць
зададзена рэкурэнтнай формулай. Знайдзіце 4 першыя элементы паслядоўнасці:
1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() ; 3)
; 3) ![]() ,
, ![]() .
.
2.25. Знайдзіце формулу агульнага элемента паслядоўнасці, у якой элементы з цотнымі нумарамі роўныя 1, а элементы з няцотнымі нумарамі роўныя 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.