Методика расчета параметров НДС
|
Рисунок 4.15 - Схема взаимодействия режущего клина с обрабатываемым материалом |
Как уже отмечалось, специфическая кинематика процесса ТТ приводит к наличию ряда особенностей процесса ТТ, которые не позволяют напрямую применить существующие методики для расчета угла сдвига, напряжений сдвига, контактных нагрузок, работы резания. В связи с этим предлагается методика для определения этих параметров.
Для простоты рассмотрим процесс прямоугольного попутного
ТТ с прямолинейной подачей. Обрабатывается поясок диаметром ![]() . Ширина пояска
. Ширина пояска ![]() . Инструмент имеет статические
передний g и задний a углы лезвия. Радиус округления РК r. Обрабатываемый материал обладает
следующими свойствами: действительный предел прочности на разрыв
. Инструмент имеет статические
передний g и задний a углы лезвия. Радиус округления РК r. Обрабатываемый материал обладает
следующими свойствами: действительный предел прочности на разрыв ![]() , предел прочности на растяжение
, предел прочности на растяжение ![]() . Частота вращения пояска
. Частота вращения пояска ![]() . Подача
. Подача ![]() .
Величина снимаемого припуска D.
.
Величина снимаемого припуска D.
Тогда в зависимости от текущего оборота ![]() толщину среза
толщину среза ![]() определяем по формуле (2.1), а
кинематические передний
определяем по формуле (2.1), а
кинематические передний ![]() и задний
и задний ![]() углы по формуле (2.8) учитывая
формулу (2.2). Тогда площадь сечения среза может
быть определена по формуле:
углы по формуле (2.8) учитывая
формулу (2.2). Тогда площадь сечения среза может
быть определена по формуле:
![]() . ( 4.45)
. ( 4.45)
Принимаем расчетную схему стружкообразования, соответствующую рисунку 4.15. Тогда мгновенная величина угла сдвига может быть определена по формулам:
– экспериментально (3.10 ):
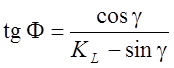 , (
4.46)
, (
4.46)
где ![]() -
экспериментально определенная усадка стружки;
-
экспериментально определенная усадка стружки;
– теоретически (см. 3.11)
![]() , (
4.47)
, (
4.47)
где 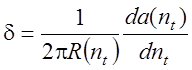 -
угол наклона поверхности резания к плоскости резания (см. рисунок 4.15);
-
угол наклона поверхности резания к плоскости резания (см. рисунок 4.15); ![]() – коэффициент, который можно
рассчитать по формуле [59]:
– коэффициент, который можно
рассчитать по формуле [59]:
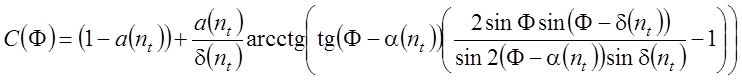 . ( 4.48)
. ( 4.48)
В этом случае коэффициент усадки стружки может быть определен из выражения (4.46) в виде:
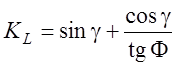 (
4.49)
(
4.49)
Угол сдвига ![]() при угле
при угле ![]() может быть определен по формуле (3.9) с коэффициентами Оксли:
может быть определен по формуле (3.9) с коэффициентами Оксли:
![]() , (
4.50)
, (
4.50)
где ![]() -
угол трения.
-
угол трения.
Степень деформации определяют по формуле (3.7):
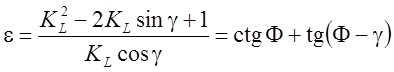 . (
4.51)
. (
4.51)
При этом площадь условной плоскости сдвига равна:
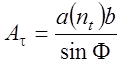 . (
4.52)
. (
4.52)
Длину контакта по передней поверхности можно определить по формуле (3.16)
![]() (
4.53)
(
4.53)
Длину пластического контакта по формуле (3.17):
![]() . (
4.54)
. (
4.54)
При этом площадь контактной площадки определяется из выражения:
![]() . (
4.55)
. (
4.55)
Сила ![]() и сопротивление
пластическому сдвигу
и сопротивление
пластическому сдвигу ![]() в условной плоскости
сдвига может быть определена из формул:
в условной плоскости
сдвига может быть определена из формул:
– экспериментально [11]
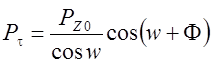 , (
4.56)
, (
4.56)
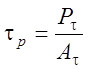 , (
4.57)
, (
4.57)
где 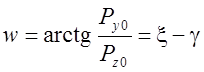 -
угол действия;
-
угол действия;
– теоретически
![]() , (
4.58)
, (
4.58)
В этом случае ![]() может быть определено из опытов на
одноосное растяжение стандартных образцов по одной из формулы (3.1). К данной
работе воспользуемся коэффициентами В. С. Кушнера:
может быть определено из опытов на
одноосное растяжение стандартных образцов по одной из формулы (3.1). К данной
работе воспользуемся коэффициентами В. С. Кушнера:
![]() , (
4.59)
, (
4.59)
где ![]() ,
1/С°.
,
1/С°.
Примем равномерное распределение касательных напряжений в условной плоскости сдвига.
Скорость сдвига ![]() определяем по
формуле (3.8):
определяем по
формуле (3.8):
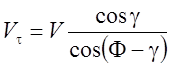 . (
4.60)
. (
4.60)
В результате главная составляющая силы на передней поверхности равна:
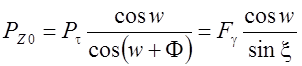 (
4.61)
(
4.61)
Тогда силы и контактные напряжения на передней поверхности можно определить по формулам :
– экспериментально (см. 2.10)
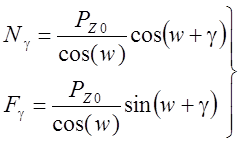 или
или 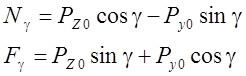 , ( 4.62)
, ( 4.62)
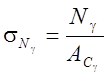 ;
; 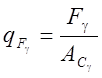 , (
4.63)
, (
4.63)
где ![]() ;
; ![]() .
.
–теоретически
![]() ,
, ![]() . (
4.64)
. (
4.64)
Поэтому в силу выражения (4.61) получим
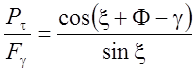 Þ
Þ
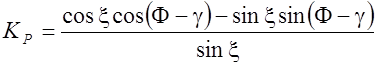 Þ
Þ
Þ 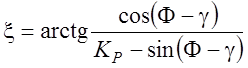 , (
4.65)
, (
4.65)
где условно принято 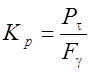 .
.
Следовательно
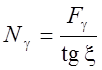 . (
4.66)
. (
4.66)
Распределение контактных напряжений вычисляем по формуле (3.15):
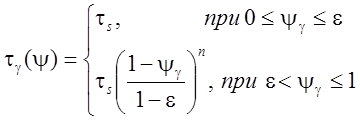 (
4.67),
(
4.67),
где 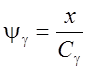 ;
;
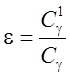 ,
, 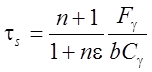
Сила трения на задней поверхности определяется по формулам:
- экспериментально из диаграмм изменения сил резания и толщины среза в течение части цикла «резание» по методике, описанной в разделе 5.
– теоретически по формуле (3.20) в виде:
![]() , (
4.68)
, (
4.68)
где 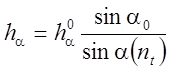 -
мгновенная ширина фаски износа (принято, что величина упругого восстановления
обработанной поверхности постоянна в процессе обработки). Принятая гипотеза,
как будет показано в разделе 5, подтверждается экспериментом.
-
мгновенная ширина фаски износа (принято, что величина упругого восстановления
обработанной поверхности постоянна в процессе обработки). Принятая гипотеза,
как будет показано в разделе 5, подтверждается экспериментом.
Тогда распределение контактных напряжений по задней поверхности может быть описано зависимостью:
![]() (
4.69)
(
4.69)
где 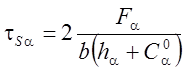 .
.
Работа деформации и трения в единицу времени определяется по формулам (3.23). Удельные работы в единицу времени деформаций, трения на передней и на задней поверхностях определяем обобщенной формуле:
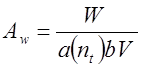 . (
4.70)
. (
4.70)
Таким образом, расчет параметров процесса НДС следует выполнять следующем порядке после экспериментального определения законов изменения сил резания, коэффициента укорочения и действительного закона изменения толщины среза:
1. Рассчитать закон изменения кинематический углов по формулам (2.8);
2. По формуле (4.46) определить закон изменения угла сдвига;
3. По формуле (4.51) определить степень деформации;
4. По формулам (4.52), (4.56) и (4.57) определить напряжения сдвига.
5. По формулам (4.53) и (4.54) определить полную длину и длину пластического контакта, а по формулам (4.62) и (4.63) силы и контактные напряжения на передней поверхности;
6. По формулам (4.67) и (4.69) рассчитываем распределение контактных напряжений;
7. По формулам (3.23) рассчитываем мощности тепловых источников и из формулы (3.22) определяем долю механической работы, идущую на изменение внутренней энергии системы.
С практической точки зрения больший интерес представляет методика теоретического расчета (прогнозирование) указанных выше параметров. В предлагаемой методике это может быть осуществлено решением системы трансцендентных уравнений (4.47) и (4.65) и далее выполнением расчетов по описанной методике.
В результате получаем все данные для проведения расчета температур методом источников, а также для анализа происходящих при ТТ процессов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.