МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО»
Кафедра «Информационные технологии»
Лабораторная работа №2
по дисциплине: «ЧИСЛЕННЫЕ МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ»
на тему: «Численное интегрирование»
Выполнила студентка гр. ИТ-31
Принял доцент
Гомель 2015
Лабораторная работа 2
Численное интегрирование
Цель работы: Научиться разрабатывать алгоритмы и проектировать программное обеспечение для численного интегрирования.
Задание на лабораторную работу
Разработать алгоритм и написать программу, реализующую следующие методы численного интегрирования.
1. Метод прямоугольников.
2. Метод Симпсона.
3. Метод интегрирования с использованием квадратурной формулы Чебышева.
Вариант 3
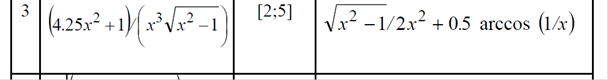
Листинг программы:
function [y]=Pervoobr(x)
y = sqrt(x.^2-1)./(2.*x.^2)+0.5.*acos(1 ./x);
endfunction
// Подинтегральнаяфункция
function [fx]=funct(x)
fx= (4.25*x.^2+1)./(x.^3*sqrt(x.^2-1));
endfunction
// Методпрямоугольников
function [S]=mrect(xf, xl, h)
xsum = 0;
del = (xl-xf)/h;
S=0;
for j= xf:del:xl
fun = funct(j);
xsum=xsum+fun;
end;
S=del*xsum;
endfunction
// МетодСимпсона
function [S]=mSimps(xf, xl, h)
xsum=0;
del = (xl-xf)/h;
S=0;
p=4;
for j=xf:del:xl
fun = funct(j);
xsum = xsum + fun*p;
p = 6 - p;
end
S = del/3*(funct(xf)+funct(xl)+xsum);
endfunction
// МетодЧебышева
function [S]=mCheb(a, b, n, t)
for i=1:1:n
x(i) = ((b+a)/2 + (b-a)/2*t(i))
end
for i=1:1:n
y(i) = funct(x(i))
end
h = (b-a)/n;
S = 0;
for i=1: 1:n
S = S + y(i);
end
S = S*h;
endfunction
// ---- Вычислениерещультатов ---- //
res = mrect(2,5,50)
disp("Метод прямоугольников")disp(res)
res = mSimps(2,5,200)
disp("Метод Симпсона")disp(res)
res = mCheb(2,5,3,[0.707107,0,-0.707107]);
disp("Метод Чебышева")disp(res)
Результат программы:

Вывод: в ходе лабораторной работы были разработаны алгоритмы, реализующие вышеперечисленные методы численного интегрирования в SciLab. Все методы дают достаточно точный результат.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.