МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО
Факультет автоматизированных и информационных систем
Кафедра «Информационные технологии»
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 1
по дисциплине «Численные методы математической физики»
на тему: «Решение нелинейных уравнений»
Выполнил: студент гр. ИТ-22
Принял: преподаватель
Гомель 2015
Цель работы: Научиться разрабатывать алгоритмы и проектировать программное обеспечение для решения нелинейных уравнений.
Задание на лабораторную работу
Разработать алгоритм и написать программу, реализующую следующие методы решения нелинейных уравнений.
1. Метод половинного деления.
2. Метод простой итерации.
3. Метод парабол.
4. Метод Гаусса
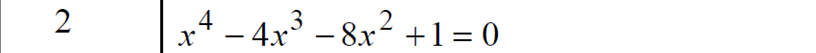
Код программы:
#include <stdio.h>
#include <math.h>
#include <iostream>
double f(double x)
{
return (2*x*x*x*x-8*x*x*x+8*x*x-1);
}
double f1(double x)
{
return (7.2*cos(3.6*x)+1);
}
double f2(double a, double b)
{
return (f(a)/(a-b)+f(b)/(b-a));
}
double f3(double a,double b, double c)
{
return (f(a)/((a-b)*(a-c))+f(b)/((b-a)*(b-c))+f(c)/((c-a)*(c-b)));
}
main()
{
setlocale(LC_ALL, "Russian");
int choose;
while(choose!=5)
{
puts("Меню:");
puts("1. Метод половинного деления");
puts("2. Метод парабол");
puts("3. Метод простой итерации");
puts("4. Решение СЛАУ");
puts("5. Выход");
printf("Выберите действие: ");
scanf("%d",&choose);
switch(choose)
{
case 1:
{
double a,b,c,eps;
printf("a=");
scanf("%lf",&a);
printf("b=");
scanf("%lf",&b);
if(f(a)*f(b)<0)
{
printf("E=");
scanf("%lf",&eps);
do
{
c=(a+b)/2;
if(f(c)*f(a)<0)
{
b=c;
}
else
{
a=c;
}
}
while(fabs(a-b)>eps);
printf("x=%.15lf f(x)=%.15lf\n",c,f(c));
}
else
{
puts("В заданном диапазоне нет корней");
}
}
break;
case 2:
{
double x0,eps,x1,x2,x3;
double w,w1;
printf("x[k-2]=");
scanf("%lf",&x1);
printf("x[k-1]=");
scanf("%lf",&x2);
printf("x[k]=");
scanf("%lf",&x3);
printf("E=");
scanf("%lf",&eps);
while (fabs(x2-x3)>eps)
{
x0=x1;
x1=x2;
x2=x3;
w=f2(x0,x1)+f2(x0,x2)+f2(x1,x2);
w1=w+sqrt(fabs(w*w-4*f(x2)*f3(x2,x1,x0)));
if(w1>0) x3=x2-(2*f(x2))/w1;
else x3=x2-(2*f(x2))/(w-sqrt(fabs(w*w-4*f(x2)*f3(x2,x1,x0))));
}
printf("x=%.15lf f(x)=%.15lf\n",x3,f(x3));
}
break;
case 3:
{
double x1,x0,eps;
printf("x1=");
scanf("%lf",&x1);
printf("E=");
scanf("%lf",&eps);
do
{
x0=x1;
x1=x0-f(x0)/f1(x0);
}
while(fabs(x0-x1)>eps);
printf("x=%.15lf\n",x1);
}
break;
case 4:
{
int i, j, n;
printf("Порядок СЛАУ: ");
scanf("%d", &n);
if(n>0)
{
double matrix[n][n+1];
for (i = 0; i < n; i++)
{
for (j = 0; j < n+1; j++)
{
printf("Элемент[%d][%d]=", i, j);
scanf("%lf", &matrix[i][j]);
}
}
puts("Матрица:");
for (i = 0; i < n; i++)
{
for (j = 0; j < n+1; j++)
{
printf("%-8.2f ", matrix[i][j]);
}
printf("\n");
}
double tmp, x[n];
int k;
for (i = 0; i < n; i++)
{
tmp = matrix[i][i];
for (j = i; j<n+1;j++)
{
matrix[i][j] /= tmp;
}
for (j = i + 1; j < n; j++)
{
tmp = matrix[j][i];
for (k = i; k <n+1; k++)
{
matrix[j][k] -= tmp*matrix[i][k];
}
}
}
x[n - 1] = matrix[n - 1][n];
for (i = n-2; i >= 0; i--)
{
x[i] = matrix[i][n];
for (j = i + 1; j <n; j++)
{
x[i] -= matrix[i][j] * x[j];
}
}
puts("Корни уравнения:");
for (i = 0; i < n; i++)
{
printf("x[%d]=%.2f\n",i,x[i]);
}
}
else puts("Неверно!");
}
break;
case 5:
{
}
break;
default:
{
puts("Неверно!");
}
break;
}
}
fflush(stdin);
return 0;
}
Результаты работы программы:
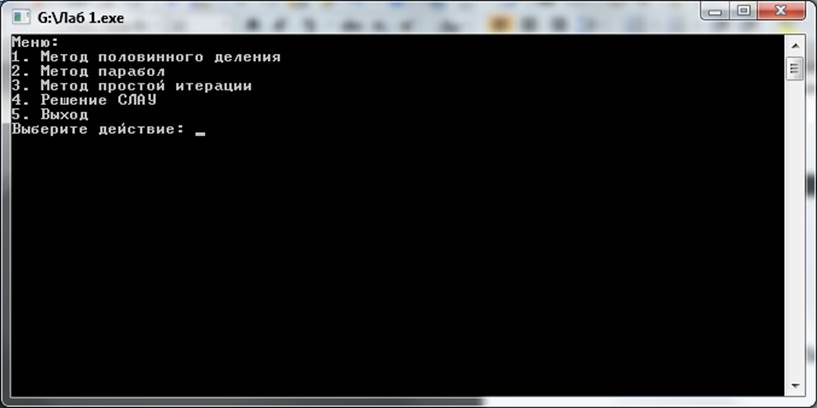
Рисунок 1 – Меню программы
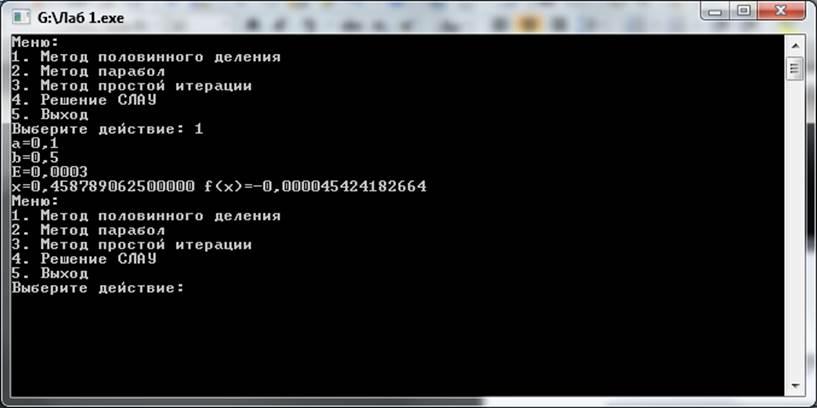
Рисунок 2 – Выполнение метода половинного деления
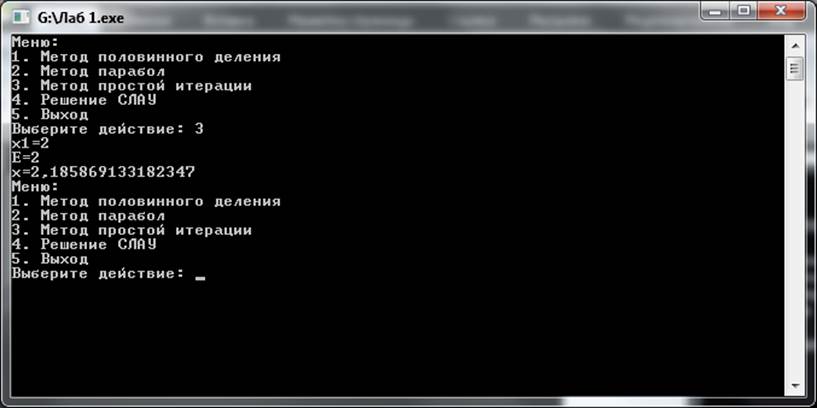
Рисунок 2 – Метод простой итерации
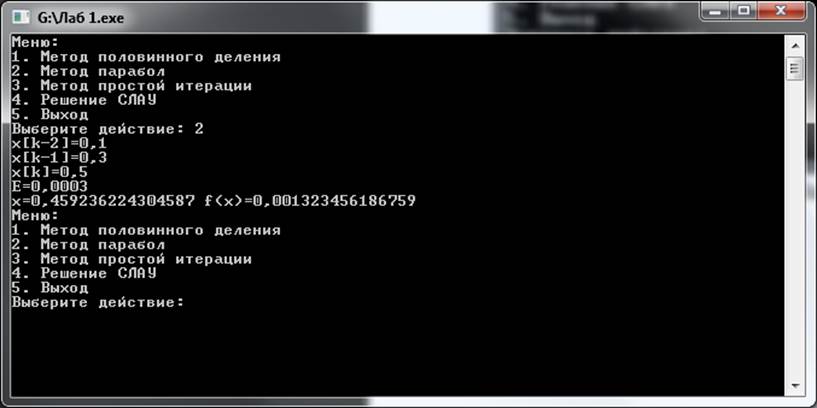
Рисунок 3 – Метод парабол
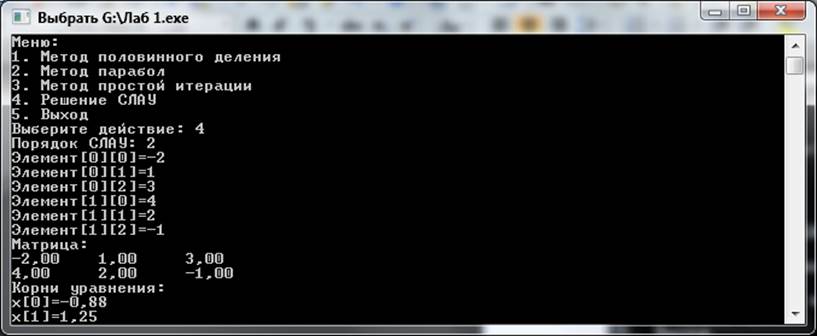
Рисунок 4 – Метод Гаусса
Вывод: в результате выполнения данной лабораторной работы научился разрабатывать алгоритмы и проектировать программное обеспечение для решения нелинейных уравнений. Был разработан алгоритм и написана программа, реализующая методы решения нелинейных уравнений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.