|
Глава 10. Динамическое программирование |
Динамическое программирование – раздел математического программирования, представляет собой метод нахождения оптимальных решений в задачах с многоэтапной (многошаговой) структурой.
Рассмотрим несколько примеров.
10.1. Задача об инвестировании предприятий
Требуется оптимальным образом распределить 120 (R=120) ед. средств между тремя предприятиями (m=3), прибыль от которых в зависимости от количества вложенных средств (х) определяется таблицей
|
Выделяемый объем средств, х |
Величина прибыли на предприятии |
||
|
f1 |
f2 |
f3 |
|
|
0 |
f1(0)=0 |
f2(0)=0 |
f3(0)=0 |
|
30 |
f1(30)=44 |
f2(30)=31 |
f3(30)=43 |
|
60 |
f1(60)=67 |
f2(60)=33 |
f3(60)=60 |
|
90 |
f1(90)=97 |
f2(90)=49 |
f3(90)=80 |
|
120 |
f1(120)=110 |
f2(120)=130 |
f3(120)=120 |
Здесь fi (xj ) – прибыль i–го предприятия при вложении в него xj средств так, чтобы суммарная прибыль со всех предприятий была максимальна.
Решение. Обозначим через ![]() количество средств, выделенных k-му предприятию. Тогда суммарная
прибыль равна сумме прибылей, полученных от каждого предприятия
количество средств, выделенных k-му предприятию. Тогда суммарная
прибыль равна сумме прибылей, полученных от каждого предприятия
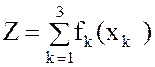 . (1)
. (1)
Очевидно, что при вложении в к-е предприятие ![]() средств мы получим прибыль fk(
средств мы получим прибыль fk(![]() ) . Неизвестные
) . Неизвестные ![]() (параметры управления) удовлетворяют ограничениям:
(параметры управления) удовлетворяют ограничениям:
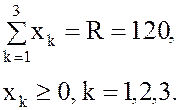 (2)
(2)
Требуется найти неизвестные
![]() , удовлетворяющие системе ограничений (2) и
обращающие в максимум функцию (1).
, удовлетворяющие системе ограничений (2) и
обращающие в максимум функцию (1).
Обычно ![]() называют оптимальным управлением.
называют оптимальным управлением.
Первый этап. Условная оптимизация
1. Разобьем процесс решения задачи на m=3 шагов (номер шага совпадает с номером предприятия).
2. Начнем оптимизацию с последнего
третьего шага. Пусть мы подошли к этому шагу с остатком средств 0≤С3≤R. Очевидно, надо вложить всю сумму С3
целиком в последнее предприятие, чтобы получить максимум прибыли. Поэтому
условное оптимальное управление на 3-м шаге - отдать последнему предприятию все
имеющиеся средства С3, т.е. ![]() , а
условная оптимальная прибыль
, а
условная оптимальная прибыль ![]() .
.
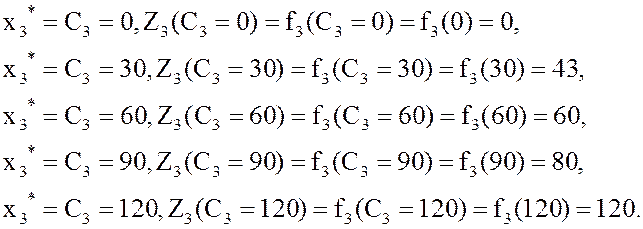
3. Перейдем к предпоследнему шагу (m-1=2). Допустимые
средства на 2-м шаге могут быть: ![]() .
.
Пусть мы подошли к этому шагу с остатком средств С2.
Обозначим ![]() условную оптимальную прибыль на
двух последних шагах (m-1=2)-м и (m =3)-м (который уже оптимизирован).
условную оптимальную прибыль на
двух последних шагах (m-1=2)-м и (m =3)-м (который уже оптимизирован).
Если мы выделим на 2-м шаге 2-му предприятию средства х2, то на последний шаг останется С3 = С2 - х2 .
Обычно Сm = Сm-1-х m-1 (m=1,2,3), где Сm –количество средств, оставшихся после к- го шага, называют уравнением состояния.
Прибыль на последних двух шагах будет составлять
![]() .
.
Нужно найти такое значение х2, при котором прибыль будет максимальна, т. е.
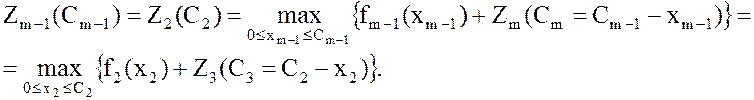
Тогда
![]() , при
, при ![]() .
.
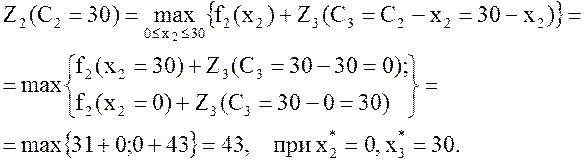
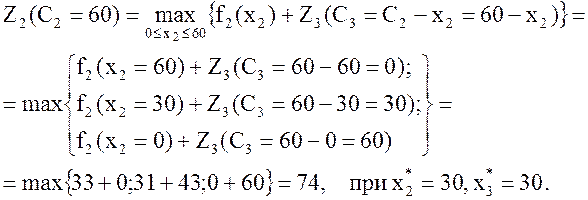
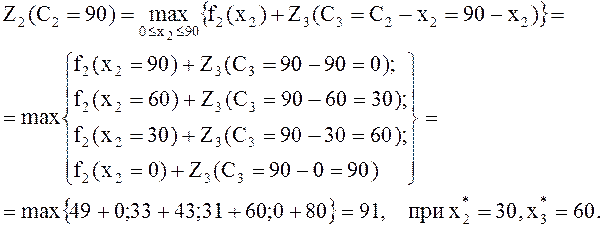
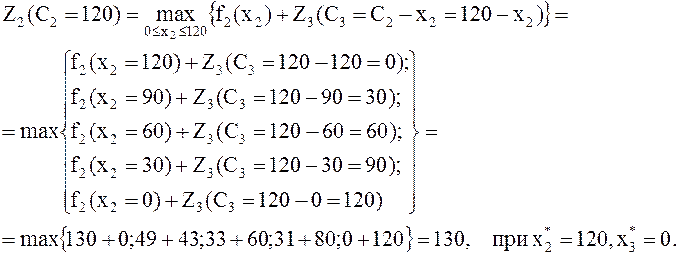
4.Перейдем к 1-му шагу, т.е. мы перейдем к 1-му предприятию. Количество средств перед первым шагом R=120, т.е. допустимое количество средств может быть только С1= 120.Тогда:
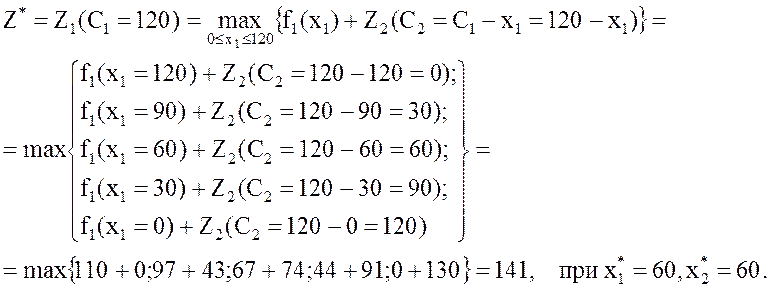
Второй этап. Безусловная оптимизация
1 шаг .k=1
С1= R =120, ![]() ,
, ![]() , т.е.
максимальный доход, который может быть достигнут при вложении R =120 ед. в три предприятии, равен 141, при этом
первому предприятию следует выделить
, т.е.
максимальный доход, который может быть достигнут при вложении R =120 ед. в три предприятии, равен 141, при этом
первому предприятию следует выделить ![]() ед.
ед.
2 шаг .k=2
На основании уравнения состояния
определяем остаток средств к началу второго шага ![]() ,
,![]() ,
,![]() , т.е. второму предприятию следует выделить
30 ед.
, т.е. второму предприятию следует выделить
30 ед.
3 шаг .k=3
![]() ,
,![]() ,
,![]() , т.е. третьему
предприятию следует выделить 30 ед. Итак, оптимальный план инвестирования
предприятий
, т.е. третьему
предприятию следует выделить 30 ед. Итак, оптимальный план инвестирования
предприятий ![]() принесет прибыль
принесет прибыль
Z* = Z1(120) = max Z = 141 ед. средств, т.е. максимум суммарной прибыли равен 141 при условии, что 1-му предприятию выделено 60 ед., 2-му и 3-му – по 30 ед. средств.
10.2. Задача о замене оборудования
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.