этом можно убедиться и прямым подсчетом, например по матричной формуле
 .
.
12. Так как показатель неэффективности стратегии q
отличается от цены игры: 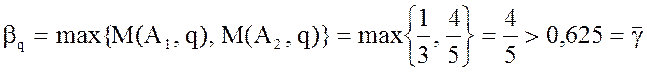 , где
, где
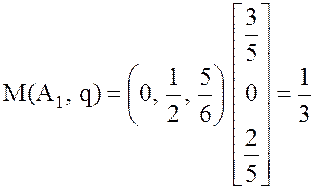 ,
, 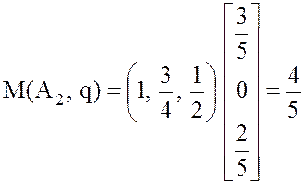 ,
,
то смесь q не является оптимальной стратегией игрока В.
11.8. Принцип доминирования
Важным примером, позволяющим уменьшить размеры платежной матрицы игры, является правило доминирования. Оно основано на отбрасывании тех чистых стратегий платежной матрицы, которые не вносят никакого вклада в искомые оптимальные смешанные стратегии. Отбрасывание подобных стратегий позволяет заменить первоначальную матрицу на матрицу меньших размеров.
Одна из возможностей снижения размеров матрицы заключается в сравнении ее строк и столбцов.
•
Считают, что i-я строка
матрицы не больше ее j-й строки, если одновременно выполняются
неравенства ![]() .
В этом случае i-я строка называется доминируемой, а j-я строка – доминирующей. При этом говорят, что стратегия Аj
игрока А доминирует стратегию Аi.
.
В этом случае i-я строка называется доминируемой, а j-я строка – доминирующей. При этом говорят, что стратегия Аj
игрока А доминирует стратегию Аi.
• Считают, что игрок А поступит разумно, если будет избегать стратегий, которым в матрице игры соответствуют доминируемые строки.
• Считают также, что k-й столбец матрицы не меньше
его ℓ-го столбца, если одновременно выполняются неравенства ![]() .
.
В этом случае k-й столбец называется доминируемым, а ℓ-й столбец – доминирующим.
При этом говорят, что стратегия Вℓ игрока В доминирует стратегию Вk.
• Считают, что игрок В поступит разумно, если будет избегать стратегий, которым в матрице игры отвечают доминируемые столбцы.
• Если в матрице игры одна из строк (один из столбцов) доминирует другую строку (другой столбец), то число строк (столбцов) в этой матрице можно уменьшить путем отбрасывания доминируемой строки (доминируемого столбца).
• Оптимальные смешанные стратегии в игре с матрицей, полученной усечением исходной за счет доминируемых строк и столбцов, дадут оптимальное решение в исходной игре.
• Вероятности, соответствующие диминируемым чистым стратегиям, следует взять равными нулю.
• При отбрасывании доминируемых строк и столбцов некоторые из оптимальных стратегий могут быть потеряны. Однако цена игры не изменится, и по усеченной матрице может быть найдена хотя бы одна пара оптимальных смешанных стратегий.
Алгоритм решения матричной игры при использовании принципа доминирования:
1. Проводится проверка наличия или отсутствия равновесия в частых стратегиях. При наличии равновесной ситуации указываются соответствующие оптимальные стратегии игроков и цена игры.
2. Проводится поиск доминируемых стратегий и усечение матрицы.
3. Ищется цена игры и оптимальные смешанные стратегии.
11.9. Методы решения игры 2´2
1. Матрица игры 2´2 имеет седловую точку
|
Вj Аi |
В1 |
В2 |
|
А1 |
а11 |
а12 |
|
А2 |
а21 |
а22 |
Если матрица имеет седловую точку, то решение игры сводится к нахождению седловой точки матрицы А. Оптимальные стратегии игроков определяются при этом координатами (i, j) седловой точки матрицы А, а цена игры – элементами аij в седловой точке (g = аij).
Пример 9. Определить оптимальное решение игры с матрицей
|
А = |
Вj Аi |
В1 |
В2 |
|
А1 |
3 |
10 |
|
|
А2 |
1 |
2 |
Решение. Определим оптимальные стратегии каждого из игроков
|
Вj Аi |
В1 |
В2 |
ai |
|
А1 |
3 |
10 |
3 |
|
А2 |
1 |
2 |
1 |
|
bj |
3 |
10 |
3 3 |
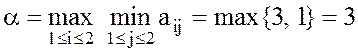 ,
, 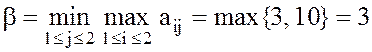 .
.
В этом примере a = b = g = 3. Таким образом, ситуация оказывается равновесной, матрица игры А имеет седловую точку a = b = g = 3. При этом оптимальны стратегии: А1 для игрока А, В1 для игрока
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.