- Справится ли касса автовокзала с потоком пассажиров? Если нет, то каково то минимальное число окон, которое необходимо для решения этой проблемы? Требуется: При известном минимальном числе окон m=mmin, необходимом для того, чтобы справиться с потоком пассажиров:
1. Построить граф состояния СМО.
2. Найти показатель эффективности СМО.
3. Найти вероятность того, что в очереди будет не более ν=2 пассажиров.
4. Определить
оптимальное количество m=mопт окон кассы, при котором относительная величина затрат Сотн ,
связанная с издержками на содержание каналов обслуживания и с пребыванием в
очереди пассажиров, задаваемая, например, как 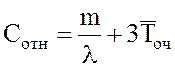 ,
будет минимальна. Сравнить показатели обслуживания при m=mmin и m=mопт.
,
будет минимальна. Сравнить показатели обслуживания при m=mmin и m=mопт.
Решение.1. Данная касса автовокзала моделируется одноканальной СМО (m=1) с неограниченной очередью.
2. Число каналов (одно касса) m=1.
3. Интенсивность входящего потока l=3 пас./мин.
4.
Среднее время обслуживания одной заявки ![]() мин.
мин.
5.
Интенсивность потока обслуживаний 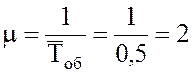 пас./мин.
пас./мин.
6.
Показатель нагрузки системы 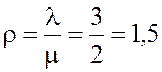 эрланга.
эрланга.
7. Нагрузка, приходящаяся на один канал 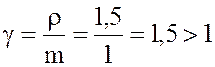 , т.е.
данная касса не справляется с потоком пассажиров на обслуживание, и со временем
количество пассажиров, приходящихся на кассу, будет неограниченно возрастать.
, т.е.
данная касса не справляется с потоком пассажиров на обслуживание, и со временем
количество пассажиров, приходящихся на кассу, будет неограниченно возрастать.
8.
Касса справится с потоком пассажиров при условии, что коэффициент нагрузки
будет меньше 1, т.е. 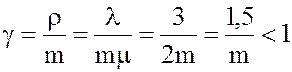 .
.
Но тогда m>1,5. Следовательно, m=2, g=0,75. Таким образом, число окон, при котором касса справится с потоком пассажиров, должно быть не менее двух (m=2).
9. Построим граф состояний двухканальной СМО (m=2) с неограниченной очередью.

Рис. 15
10. Вероятность того, что в системе нет ни одной заявки, равна вероятности того, что обе кассы свободны:
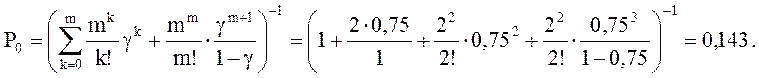
11. Вероятность состояния системы равна вероятности того, что у касс обслуживаются один или два пассажира:
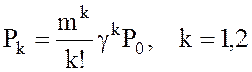 ,
,
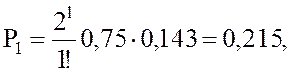
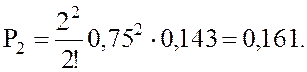
Вероятность того, что в очереди стоят 1, 2, 3 или 4 и т.д. пассажира, определяется так:
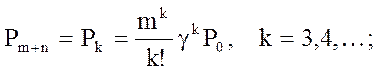
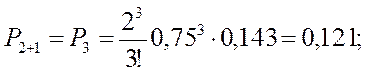
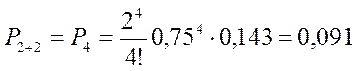 ит.д.
ит.д.
12. Вероятность отказа Ротк = 0.
13. Вероятность того, что заявка будет принята в СМО: Рсист = 1-Ротк =1.
14. Относительная пропускная способность q = Рсист = 1-Ротк =1.
15. Вероятность того, что заявка окажется в очереди:
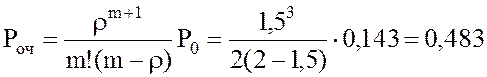 .
.
16. Абсолютная пропускная способность A = λ∙q = 3∙1 = 3.
17.
Среднее число занятых кассиров (среднее число обслуживаемых пассажиров) ![]() .
.
18. Среднее число пассажиров в очереди
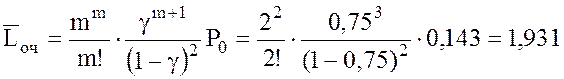 .
.
19. Среднее число пассажиров у кассы
![]() .
.
20. Среднее время, которое пассажир проводит в очереди:
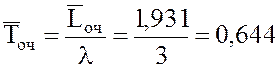 мин.
мин.
21. Среднее время, которое пассажир тратит на приобретение билета (среднее время, которое заявка проводит в системе):
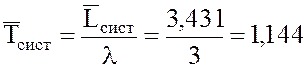 мин.
мин.
22. Вероятность того, что обслуживания ожидают не более n=2 заявок (вероятность того, что в очереди не более n=2 пассажира):
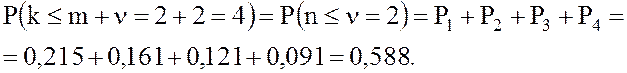
23. Коэффициент (доля) занятых обслуживанием окон
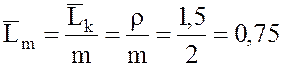 .
.
24. Относительная величина затрат при m=2
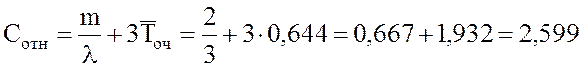 .
.
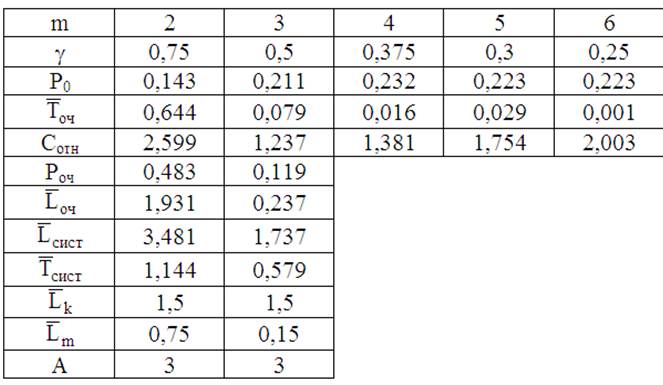
25. Рассчитаем относительную величину затрат при других значениях m (табл. 3).
26. Минимальные затраты получены при m = mопт = 3 окнам кассы (см. табл. 3, в которой
показаны показатили эффективности). Как видим, при m = 3
по сравнению с m = 2 существенно уменьшилась вероятность
возникновения очереди Роч, длина очереди ![]() и
среднее время пребывания в очереди
и
среднее время пребывания в очереди ![]() . Соответственно
уменьшились: среднее число пассажиров
. Соответственно
уменьшились: среднее число пассажиров ![]() ,
среднее время нахождения у окон
,
среднее время нахождения у окон ![]() , а также доля занятых
обслуживанием окон
, а также доля занятых
обслуживанием окон ![]() . Но
. Но ![]() и А не
изменились.
и А не
изменились.
Таблица 3
27. Вероятность того, что в очереди будет не более 2 пассажиров:
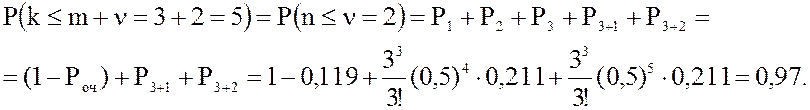 Заметим, что в случае m = 2 та же вероятность существенно меньше:
Заметим, что в случае m = 2 та же вероятность существенно меньше:
![]() .
.
Пример 10. - Билетная касса работает без перерыва.
- Данная касса имеет два окошка, в каждом из которых продаются билеты в два пункта Х и Y.
- Среднее число пассажиров, желающих приобрести билеты в кассе, для обоих пунктов одинаково: lх = ly = 0,3 пасс./мин.
-
Время, которое тратит касир на обслуживание одного пассажира, в среднем равно ![]() мин.
мин.
- Все потоки в системе простейшие.
- Рассматриваются два варианта продажи билетов:
а) билеты продаются в одной кассе с двумя окошками одновременно в оба пункта Х и Y;
b) билеты продаются в двух специализированных кассах (по одному окошку в каждой), одна - только в пункт Х, другая – в пунктY.Необходимо:
1. Сравнить два варианта продажи билетов по осоновным показателям
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.