Решение многокритериальной задачи с использованием данных таблицы и линейной свертки

Задание по теме лекции №1

1. Найти решение многокритериальной задачи, используя данные таблицы и линейную свертку.

Таблица

Критерии эффективности задачи ИО

2. Используя данные

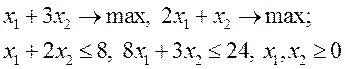
и метод контрольных показателей, найти решение многокритериальной задачи.

3. Используя данные таблицы и метод метрики в пространстве состояний (формулы (1.6), (1.7)), найти решение многокритериальной задачи.

Контрольные вопросы

1. Какие существуют методы преодоления неопределенности целей в многокритериальных задачах ИО?

2. Пояснить особенности метода контрольных показателей при сведении задачи к линейному программированию.

3. Существуют ли случаи (если да, то привести примеры), когда возможно достижение точки абсолютного экстремума в пространстве критериев?

4. Существуют ли случаи (если да, то привести примеры), когда возможно равенство решений по формулам (1.6), (1.7)?

Задание по теме 2

1. Определить значения множества Парето х для уравнения  и вариантов критериев, заданных в таблице.

Таблица

Критерии эффективности задач ИО

Вариант 1	Вариант 2	Вариант 3	Вариант 4

2. Численно построить множество Парето для условий таблицы Лабораторной работы № 1. Начальные точки С₁ и С₂ и последующие определить из графика в системе координат . Численное множество Парето должно содержать не менее 6 точек.

Контрольные вопросы

1. Дать определение множества Парето и выбора оптимального по Парето решения.

2. Пояснить алгоритм численного построения множества Парето.

3. Является ли оптимальное решение оптимальным по Парето?  Дать развернутые пояснения.

Задание по теме 3

Решить задачу линейного и квадратичного программирования.

1. Имеется 3 пункта производства и 5 пунктов потребления. Объемы производства в пунктах А₁, А₂, А₃ равны соответственно 167, 93, 150 ед., и потребность продукции в пунктах В₁, В₂, В₃, В₄, В₅ равна соответственно 92, 68, 80, 75, 95. Стоимость перевозки одной единицы продукции из А_i в В_j дана в матрице С.

.

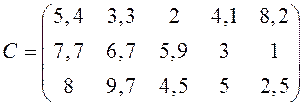Требуется найти оптимальный план перевозок, минимизирующий суммарную их стоимость при соблюдении дополнительных условий табл. 3.1.

2. На некотором предприятии планируется производство двух новых продуктов x₁ и x₂. Их предполагаемая цена составляет p₁ и p₂ соответственно. Затраты на приобретение, доставку сырья, а также производство продукции оцениваются следующим соотношением: 0,5(x₁² + x₂²) + 0,3x₁x₂. Таким образом, функция прибыли может быть записана

.

                                                                                                    Таблица 3.1

Дополнительные ограничения на перевозки из пункта А_i в пункт

потребления В_j

Параметр	Вариант
	1	2	3	4	5	6	7
Тип перевозки	A1B1	A1B2	A1B1	A1B3	A2B1	A1B3	A1B4
Ограничение	≥ 50	≥ 45	≥ 55	≥ 50	≤ 30	≥ 55	≥ 45
Тип перевозки	A3B5	A3B4	A2B5	A3B5	A2B5	A2B1	A3B3
Ограничение	≥60	≥65	≥40	≥65	≥60	≤20	≥45
Тип перевозки	A2B4	A2B3	A3B4	A2B1	A3B4	A2B4	A3B2
Ограничение	≤40	≤40	≤45	≤30	≤50	≤60	≤20

Также известно, что на производство 1000 шт. первого продукта требуется сумма s₁⁰млн. руб. от основных фондов и s₁^Тмлн. руб. от других ресурсов, а для второго – s₂⁰и s₂^Т соответственно. Для производства этих продуктов не может быть потрачено средств основных фондов свыше s⁰_max и других ресурсов – свыше s^Т_max.

Требуется найти оптимальное соотношение плана выпуска x₁ и x₂ с учетом данных табл. 3.2.

                                                                                                                      Таблица 3.2

Исходные данные