Основные принципы классической термодинамики установлены в результате наблюдений, проводившихся в течении двух веков. Эти эксперименты, выполнявшиеся почти исключительно для объемных фаз, показали, что макроскопические системы в отсутствии возмущений спонтанно стремятся к состоянию равновесия, характеризуемому малым числом термодинамический переменных. Изучение поверхности твердых тел началось значительно позже; соответственно в этой области накоплено меньше экспериментальных фактов.
Вопрос: должна ли лежать в основе рассмотрения нашей проблемы независимая термодинамика поверхностей. Этим вопросом занимался Гиббс.
Основные положения термодинамики конечных объемов вещества могут быть сформулированы очень кратко. В равновесии однокомпонентная система полностью характеризуется величиной внутренний энергии U, которая является однозначной функцией энтропии (S), объёма (V) и числа частиц (N) системы:
U = U (S, V, N) (1.1)
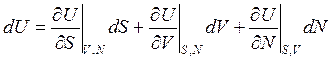
dU = TdS – PdV + µdN
Эти уравнения определяют температуру (T), давление (P) и химический потенциал (µ) объёмной фазы. Используя свойство экстенсивности внутренний энергии
U(λS, λV, λN) = λU(S, V, N) (1.2)
в сочетании с первым и вторыми законами, с помощью теоремы Эйлера получаем уравнение
U = TS – PV + µN. (1.3)
Дифференцируя (1.3) и используя (1.1), приходим к соотношению между интенсивными переменными, известному как уравнение Гиббса-Дюргейма:
SdT – VdP - Ndµ = 0 (1.4)
Как должны изменится приведенные выше рассуждения для системы со свободной поверхностью? Приготовим поверхность площадью А посредством раскола бесконечно твердого тела. Так как в объемной фазе не происходит самопроизвольного раскалывания, полная энергия системы должна возрасти на величину, пропорциональную А. Коэффициент пропорциональности γ называется поверхностным натяжением:
U = TS – PV + µN + γA. (1.5)
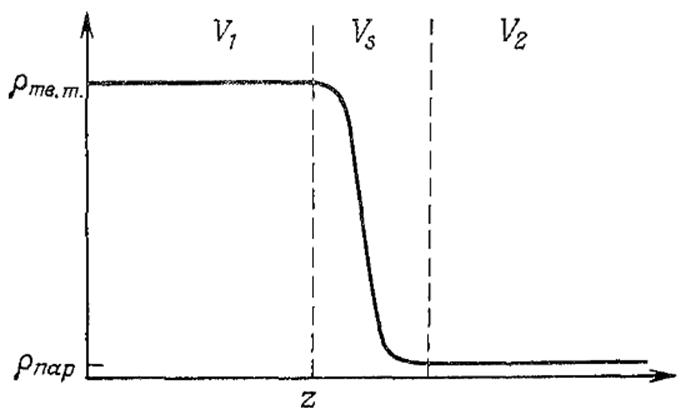
Рис.1.1. Распределение плотности в однокомпонентной системе в зависимости от расстояния до поврности.
В равновесии при любых конечных температуре и давлении полубесконечное твердое тело сосуществует со своими парами. Зависимость числа частиц от расстояния, измеренного перпендикулярно поверхности, показана на рис.1.1. Гиббс обнаружил, что удобно относить определенные значения экстенсивных переменных к некоторой площади поверхности. В соответствии с этим вертикальные линии на рис.1.1 делят пространство на область твердого тела, область паров и переходную область или поверхность. Оставшиеся экстенсивные величины можно представить следующим образом:
S = S1 + S2 + S3, (1.6)
V = V1 + V2 + V3,
N = N1 + N2 + N3.
В этих формулах объёмные параметры определены как
Si = siVi
Ni = ρiVi i = 1,2
где si и ρi характеризуют однородные объёмные фазы. В соответствии с (1.6) если поверхности объемных фаз выбраны, то остальные величины, относящиеся к поверхности раздела, определяются как избытки. Заметим, что изменения поверхностных избыточных величин полностью определяются изменениями объёмных величин:
ΔSs = - ΔS1 – ΔS2, (1.8)
ΔVs = - ΔV1 – ΔV2,
ΔNs = - ΔN1 – ΔN2
Очевидно, что конкретный выбор положения границ на рис. 1.1 неоднозначен. Тем не менее выясняется, что всегда можно выбрать подмножество поверхностных избытков, которые являются полностью определяемыми параметрами, причем их значения не зависят от положения некоторой удобно выбранной границы раздела.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.