Тема 4. Вычисление определенного интеграла.
Задание 1.
1. Привести квадратурную
формулу средних прямоугольников для приближенного вычисления интеграла ![]() ,
выражение для остаточного члена и его оценку для достаточно гладких функций.
Сформулировать правило Рунге для практической оценки погрешности этой формулы и
указать класс функций, для которых оно теоретически обосновано.
,
выражение для остаточного члена и его оценку для достаточно гладких функций.
Сформулировать правило Рунге для практической оценки погрешности этой формулы и
указать класс функций, для которых оно теоретически обосновано.
2. Составить программу, реализующую вычисление интеграла с помощью формулы из п.1 с заданной точностью e. Точность формулы оценивать по правилу Рунге.
Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.
Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, Sk – приближенное значение интеграла.
3. Используя составленную программу, вычислить интеграл
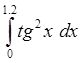 с
точностью e=10-4. (*)
с
точностью e=10-4. (*)
Вычислить аналитически точное значение интеграла и погрешность его приближения Sk. Пользуясь теоретической оценкой погрешности формулы (п.1), найти число узлов, обеспечивающее ту же точность вычисления интеграла (*).
Литература.
1. Волков Е.А. Численные методы. М.1982.
Тема 4. Вычисление определенного интеграла.
Задание 2.
1. Привести составную
квадратурную формулу трапеций (СКФТ) для приближенного вычисления интеграла ![]() ,
выражение для ее остаточного члена и его оценку для достаточно гладких функций.
Сформулировать правило Рунге для практической оценки погрешности этой формулы и
указать класс функций, для которых оно теоретически обосновано.
,
выражение для ее остаточного члена и его оценку для достаточно гладких функций.
Сформулировать правило Рунге для практической оценки погрешности этой формулы и
указать класс функций, для которых оно теоретически обосновано.
2. Составить программу, реализующую вычисление интеграла по СКФТ с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге. Предусмотреть в программе экономизацию вычисления квадратурной суммы при переходе к половинному шагу.
Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.
Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, Sk – приближенное значение интеграла.
3. Используя составленную программу, вычислить интеграл
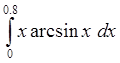 с
точностью e=10-5. (*)
с
точностью e=10-5. (*)
Вычислить аналитически точное значение интеграла и погрешность его приближения Sk. Пользуясь теоретической оценкой погрешности формулы (п.1), найти число узлов, обеспечивающее ту же точность вычисления интеграла (*).
Литература.
1. Бахвалов Н.С. Численные методы., Наука, М.1973.
2. Волков Е.А. Численные методы. М.1982.
Тема 4. Вычисление определенного интеграла.
Задание 3.
1. Привести составную
квадратурную формулу Симпсона (СКФС) для приближенного вычисления интеграла ![]() ,
выражение для ее остаточного члена и его оценку для достаточно гладких функций.
Сформулировать правило Рунге для практической оценки погрешности этой формулы и
указать класс функций, для которых оно теоретически обосновано.
,
выражение для ее остаточного члена и его оценку для достаточно гладких функций.
Сформулировать правило Рунге для практической оценки погрешности этой формулы и
указать класс функций, для которых оно теоретически обосновано.
2. Составить программу, реализующую вычисление интеграла по СКФС с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге. Предусмотреть в программе экономизацию вычисления квадратурной суммы при переходе к половинному шагу.
Входные данные программы: a, b, f, e; n – начальное число узлов; m – предельное число узлов.
Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, Sk – приближенное значение интеграла.
3. Используя составленную программу, вычислить интеграл
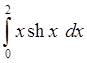 с
точностью e=10-4. (*)
с
точностью e=10-4. (*)
Вычислить аналитически точное значение интеграла и погрешность его приближения Sk.
Пользуясь теоретической оценкой погрешности формулы (п.1), найти число узлов, обеспечивающее ту же точность вычисления интеграла (*).
Литература.
1. Волков Е.А. Численные методы. М.1982.
Тема 4. Вычисление определенного интеграла.
Задание 4.
1. Привести составную
квадратурную формулу Гаусса (СКФГ) для приближенного вычисления интеграла ![]() ,
выражение для ее остаточного члена и его оценку для достаточно гладких функций.
Сформулировать правило Рунге для практической оценки погрешности этой формулы и
указать класс функций, для которых оно теоретически обосновано. В качестве
основной использовать КФГ с 2 узлами; координаты этих узлов для отрезка
[-1, 1] и соответствующие им коэффициенты взять из книги [1]. Шаг разбиения
отрезка [a, b] – постоянный.
,
выражение для ее остаточного члена и его оценку для достаточно гладких функций.
Сформулировать правило Рунге для практической оценки погрешности этой формулы и
указать класс функций, для которых оно теоретически обосновано. В качестве
основной использовать КФГ с 2 узлами; координаты этих узлов для отрезка
[-1, 1] и соответствующие им коэффициенты взять из книги [1]. Шаг разбиения
отрезка [a, b] – постоянный.
2. Составить программу, реализующую вычисление интеграла по СКФГ (с двумя узлами в основной формуле) с заданной точностью e. Точность (погрешность) формулы оценивать по правилу Рунге.
Входные данные программы: a, b, f, e; n – начальное число отрезков разбиения отрезка [a, b]; m – предельное число этих отрезков.
Выходные результаты: k – число узлов, обеспечивающее заданную точность вычисления интеграла, Sk – приближенное значение интеграла.
3. Используя составленную программу, вычислить интеграл
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.