ІІ. Завдання до міжвузівської математичної олімпіади
№1. Знайдіть всі розв’язки у цілих числах рівняння
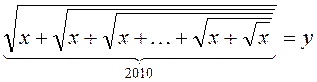
Розв’язання.
Після
піднесення обох частин рівняння до квадрату і перенесення в праву частину, ми
переконуємося в тому, що корінь, який залишається в лівій частині, дорівнює у2–х,
тобто представляє собою ціле число. Повторюючи це міркування, ми
врешті-решт переконаємося в тому, що ![]() і
і ![]() повинні бути цілими числами, звідки x=k2 ,
повинні бути цілими числами, звідки x=k2 , ![]() тобто
тобто ![]() . Остання рівність неможлива при
. Остання рівність неможлива при ![]() , оскільки k2 менше k(k+1), а (k+1)2 вже більше k(k+1) і тому
, оскільки k2 менше k(k+1), а (k+1)2 вже більше k(k+1) і тому ![]() , тобто не може бути цілим.
Відповідь. Єдине рішення рівняння в цілих числах - х = 0; у=0.
, тобто не може бути цілим.
Відповідь. Єдине рішення рівняння в цілих числах - х = 0; у=0.
№2. Дано n додатніх чисел ![]() таких, що
таких, що ![]() .
.
Доведіть, що
![]()
Розв’язання. Маємо: 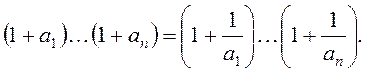
Отже,
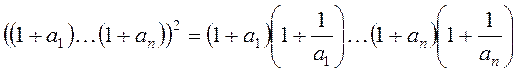
Оскільки
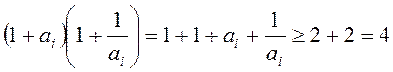 , то
, то
![]() .
.
№3. Знайдіть всі функції f(x), що задовольняють рівнянню
![]()
для будь-яких дійсних х і у. Доведіть, що тільки дві з них неперервні.
Розв’язання. Нехай в даному рівнянні у=х, тоді
![]() , звідки при х≠0
, звідки при х≠0 ![]() ,
отже, або
,
отже, або ![]() , або
, або ![]() .
.
Нехай ![]() при х=а≠0, тоді з даного рівняння
одержуємо
при х=а≠0, тоді з даного рівняння
одержуємо ![]() для
всіх у, тобто
для
всіх у, тобто ![]() .
.
Нехай ![]() при х=а≠0, тоді з даного рівняння
одержуємо
при х=а≠0, тоді з даного рівняння
одержуємо ![]() , звідки
, звідки ![]() при у≠0, а при у=0
при у≠0, а при у=0 ![]() - будь-яке число.
- будь-яке число.
Отже, всі рішення даного функціонального рівняння наступне:
1) ![]() .
.
2) Кожна функція вигляду
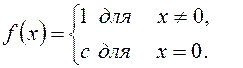
Серед цих рішень
тільки функції ![]() і
і![]() є
неперервними.
є
неперервними.
№4. Встановити, чи існує многочлен Р(x), для якого при будь-якому дійсному x одночасно виконуються нерівності: ![]() і
і ![]() .
.
Розв’язання. Якщо Р(х) – константа, то ![]() , і нерівність 1) не виконана. Нехай
, і нерівність 1) не виконана. Нехай ![]() , тоді якщо n
непарне, то
, тоді якщо n
непарне, то ![]() – непарне число, звідки
– непарне число, звідки
![]() хоча б в одній точці
хоча б в одній точці ![]() , якщо ж n парне, то
, якщо ж n парне, то ![]() -
непарне число, звідки
-
непарне число, звідки ![]() хоча б в одній точці
хоча б в одній точці ![]() . Таким чином, для будь-якого многочлена Р(х)
не виконана або нерівність 2), або нерівність 1).
. Таким чином, для будь-якого многочлена Р(х)
не виконана або нерівність 2), або нерівність 1).
Твердження доведено.
№5. Нехай кількість людей збільшується щорічно на 1 / 100 свою частину. Через скільки років число людей збільшиться у 10 разів?
Розв’язання. Припустимо, що це наступить через х
років, причому число людей спочатку дорівнювало n; таким чином, черех х років воно
буде дорівнювати 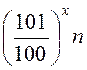 , а оскільки воно повинно
дорівнювати 10n, то
, а оскільки воно повинно
дорівнювати 10n, то
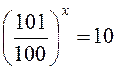 ;
;
тому
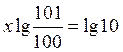
і
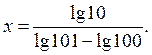
Таким чином, маємо
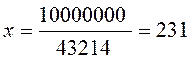 приблизно.
приблизно.
Отже, через 231 рік число людей, якщо щорічне прирощення складає тільки 1/100 частину, збільшиться у 10 разів.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.